铺面工程学（第2版）-弹性多层结构轴对称模型及理论解

1.一般概念

路面结构可以看作一种多层结构，图6-2是这种结构在圆形均布荷载作用下应力应变场的一般概念描述。图6-2中，h1、E1、μ1，h2、E2、μ2，…，hn-1、En-1、μn-1分别为结构的第一层、第二层、…、第n-1层的厚度、弹性模量和泊松比，E0、m0为路基的弹性模量和泊松比，p和δ分别为垂直荷载的压力集度和作用半径。

对图6-2所示的路面结构，在进行力学分析时一般做如下假设：

（1）路面结构由多个性能不同的层次组成，在圆形均布荷载的作用下，呈现轴对称的特性。

（2）每个层次都是由均质的、各向同性的线弹性材料组成，材料性能可采用弹性模量E和泊松比μ表征。

（3）结构的最下层为在水平方向上无限大、竖向（z方向）向下无限深的半无限体，且无限深度处的应力和位移为零；其上各层为在水平方向上无限大、z方向上有一定厚度的层次。

（4）各层间接触条件可以有多种状况：层间位移完全连续，此时称为连续体系；层间竖向（z方向）应力和位移连续、水平摩擦力为零，此时称为滑动体系；层间竖向应力和位移连续、水平摩擦力不为零，此时称为半连续体系。

图6-2所示的是圆柱坐标系统（r，θ，z），弹性单元体内微小六面体上的应力分量共有9个，包括3个法向应力σr，σθ，σz和3对剪应力τrz=τzr，τrθ=τθr，τzθ=τθz。由于图6-2是关于z轴的轴对称结构，各应力、应变和位移分量也关于该轴对称，并且是r和z的函数，此时τrθ=τθr=0，τzθ=τθz=0。

在圆柱坐标系统中，各点应力、应变的物理方程为

图6-2　轴对称弹性多层结构的一般概念

式中　εr，εθ，εz——分别为单元体的正应变；

γzr——单元体的剪应变；

G——单元体的剪切弹性模量。

根据单元体的各应力分量，可按下面的一元三次方程式求解单元体的三个主应力：

式中　I1——第一应力不变量，；

I2——第二应力不变量，；

I3——第三应力不变量，。

解出式（6-2）的三个实根，从大到小记为σ1，σ2，σ3，即为单元体的三个主应力。然后，可按式（6-3）计算该单元体的最大剪应力：

上述工作均可由计算机来完成。国内如同济大学、广西壮族自治区交通运输厅、哈尔滨建筑大学（前身为哈尔滨工业大学土木建筑系）等已研发了若干种软件，既可用于应力与位移的计算，也可用于沥青路面的设计。国外更有多种软件，如表6-1所列［1］。

表6-1　国外几种多层弹性体系分析计算机程序

为了更好地理解路面结构的力学计算过程，分析不同因素对结构的应力、应变和位移的影响，下面介绍两层、三层层间连续路面结构的手工计算方法。

2.两层路面结构的力学计算

假定路基为弹性半无限体，上面的路面结构层为材料的弹性参数与路基不同的均匀层次，这便构成了一个两层路面结构，或称双层路面结构，如图6-3所示。

图6-3　双层路面结构

利用弹性理论，可得图6-3双层路面结构在荷载集度为p、半径为δ的竖向圆形均布荷载作用下，距荷载作用面中心轴r处的路面竖向位移，即路面弯沉：

式中　E0——路基弹性模量，MPa；

——双层路面结构表面距荷载作用面中心轴r处的弯沉系数，为r/2δ，h/（2δ）和E0/E1的函数：

式中　E1——上层材料的弹性模量，MPa；

h——上层材料的厚度，cm。

式（6-5）是一个包含了贝塞尔函数的广义积分式。1943年，D.M.Burmister首先提出了双层结构的解，并给出了μ=0.5，r=0处的弯沉系数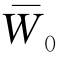的计算诺谟图。同济大学公路工程研究所［2］采用μ0=0.35，μ1=0.25，解算了r=0处的弯沉系数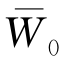的数值，并绘制了诺谟图，如图6-4所示。

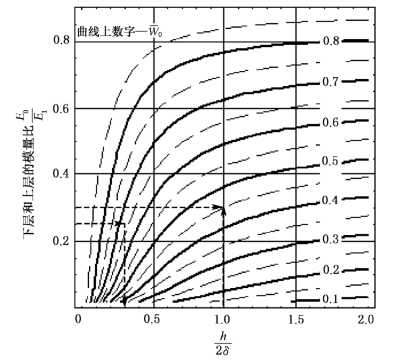
图6-4　双层连续结构荷载中轴处路面表面弯沉系数诺谟图

【例6-1】已知p=0.7 MPa，δ=10 cm，E0=45 MPa，E1=180 MPa，h=20 cm。求荷载作用面中轴处的弯沉W0。

【解】

由图6-4纵轴E0/E1=0.25处引水平线，横轴h/（2δ）=1.0处引竖直线，在两线交点处内插出=0.42。

根据式（6-4），

【例6-2】已知p=0.5 MPa，δ=10 cm，E0=65 MPa，E1=280 MPa，荷载面中轴处的弯沉值W0限定为1 mm。求面层应有的厚度h1。

【解】根据式（6-4）得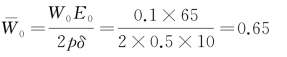

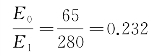
从图6-4的纵轴E0/E1=0.232处引一水平线，同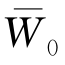=0.65的曲线相交，从交点作一垂线与横轴相交，交点处h/（2δ）=0.3。由此，可得面层应有厚度为h1=6 cm。

【例6-3】条件如例6-1，若将该两层路面结构看作均质弹性半空间体，求其等效模量。

【解】假定半空间体的泊松比μ=0.35，则在圆形均布荷载作用下中心点的弯沉为：

根据【例6-1】的条件，可知弯沉为0.131 cm，采用弯沉相等作为等效原则，故可求得E=94 MPa。

3.三层路面结构的力学计算

一般而言，交通量越大、轴载越重，路面结构的层次越多。如果根据各层次的功能和材料的特性，将路面结构划分为面层、基层和路基三个层次，便形成了典型的三层路面结构［3］，如图6-5所示。

图6-5　三层路面结构　

(www.xing528.com)

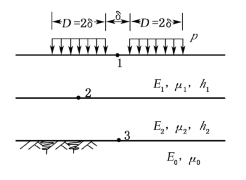
图6-6　双圆垂直荷载下的计算图式

1945年，D.M.Burmister提出了三层结构在一个圆形均布垂直荷载作用下应力和位移的一般解。但载重汽车的后轮多为双轮组荷载，我国《公路沥青路面设计规范》（JTGD50—2017）规定的标准荷载也为双轮荷载，所以在路面分析和设计时应采用双圆荷载的计算图式，如图6-6所示。为了方便，此时假定双圆圆心之间的距离为3δ。

双圆荷载模式破坏了荷载的轴对称性，所以计算时可采用单圆荷载，并采用叠加法计算双圆荷载作用下路面结构的力学响应（应力、应变和位移）。在D.M.Burmister的一般理论解的基础上，同济大学公路工程研究所［2］采用μ1=μ2=0.25和μ0=0.35，求得了图6-5所示结构中若干特征点应力、应变和位移分量的数值解，按照式（6-2）将各应力分量转换为最大主应力值，并采用叠加法编绘出图6-6所示三层连续结构双轮轮隙中点（点1）处的表面弯沉系数诺谟图和上层底面（点2）、中层底面（点3）处的主应力系数诺谟图。

图6-6上点1的弯沉和点2、点3的主应力值可按下式计算：

式中　W0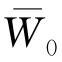，——双轮荷载轮隙中点的路表弯沉和弯沉系数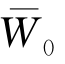，由图6-7计算；

σ12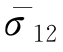，——上层底面（点2）的主应力和主应力系数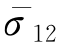，由图6-8计算；

σ13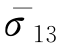，——中层底面（点3）的主应力和主应力系数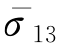，由图6-9计算。

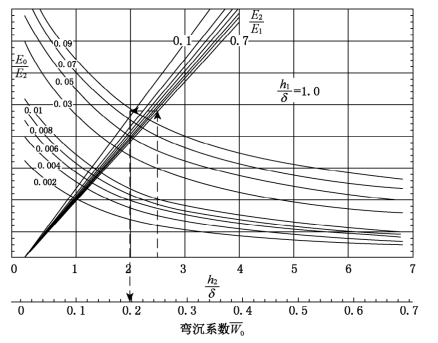
图6-7　三层连续结构双轮荷载轮隙中点处的表面弯沉系数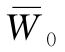诺谟图

图6-8　三层连续结构上层底面单轮中心处（点2）的主应力系数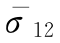诺谟图

【例6-4】已知p=0.5 MPa，双圆荷载，δ=10 cm，E0=270 MPa，E2=3 000 MPa，E1=6 000 MPa，h2=25 cm，h1=10 cm。求轮隙中点表面弯沉W0、面层和基层底面的主拉应力σ12和σ13。

【解】

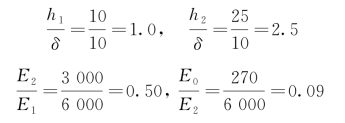
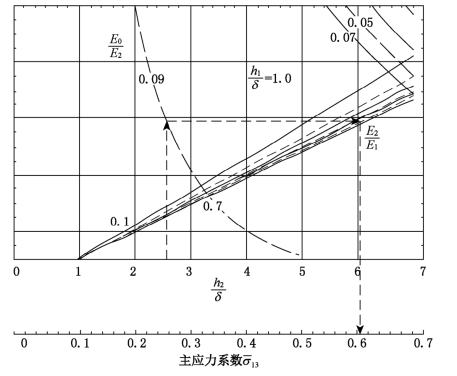
图6-9　三层连续结构中层底面双轮轮隙中心（点3）处的主应力系数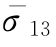诺谟图

根据图6-7的查图示意，即由h2/δ=2.5，E0/E2=0.09和E2/E1=0.5，可查得W0=0.200，由式（6-7）可得表面弯沉值为

根据图6-8的查图示意，即由h2/δ=2.5，E0/E2=0.09和E2/E1=0.5，可查得=0.164，由式（6-8）得面层底面的主拉应力为

σ12=p·=0.5×0.164=0.82 MPa

根据图6-9的查图示意，即由h2/δ=2.5，E0/E2=0.09和E2/E1=0.5，可查得=0.602，由式（6-9）得基层底面的主拉应力为

σ13=p·=0.5×0.602=0.301 MPa

4.多层结构的换算

为了了解路面工程中解决问题的常用方法，这里介绍一下采用图6-10—图6-12中的图表计算多层路面结构的弯沉的方法。

当路面结构仅为两层或三层时，可以采用上述图表直接计算路面临界点的弯沉值和应力值。随着路面结构层次的增加，几何参数和模量参数也相应增多，采用图表法难以简洁地表达不同情况下的计算结果。所以，对于多层（层数n＞3）结构，可以根据计算机的计算结果，采用一些简化计算但又不过多影响精度的近似方法，把n层路面结构转化为等效的三层结构，然后利用三层结构理论解的诺谟图来计算n层结构的弯沉和应力。

在相同轴载条件下，影响路面结构弯沉或应力的因素主要是各结构层的弹性参数（模量、泊松比）和厚度。具有某一模量和厚度的结构层，可以等效地换算为具有另一种模量和厚度的结构层而使其弯沉或应力保持不变。如果能找到一个比较稳定的换算关系，就可以把n层结构中的某些结构层换算成与其相邻层模量相同的等效层，从而使n层路面结构转化为三层结构，并采用三层结构的诺谟图计算原路面结构的弯沉或应力。这便是路面结构等效换算的基本原理，这个过程称为路面结构的等效（当量）换算。

等效换算关系是通过将n层结构的精确解与等效三层结构计算结果进行对比、分析和归纳而得的。由于路面结构层的弹性参数和厚度对应力和位移量的影响程度不同，因而难以找到一个适用于各个力学指标的统一的换算关系。所以，针对不同的路面设计指标，通过计算和分析分别建立了适用于这些指标的等效换算关系［46］，使n层路面结构可以转化为三层结构。

基于路面临界弯沉指标的多层路面结构等效换算方法如图6-10和式（6-10）所示，即面层的模量和厚度、基层的模量和厚度以及路基的模量保持不变，路基与基层之间的各层均换算成模量为基层的材料，求其等效厚度，并与基层厚度叠加，形成一个等效的三层结构。

图6-10　针对路表回弹弯沉指标的路面结构等效换算

式中　H2——换算后的等效三层结构的第二层的厚度；

hi，Ei——分别为原n层结构中第i层的厚度和模量。

【例6-5】［3］现有一五层结构，已知各层的模量和厚度（表6-2），请转化成三层结构，以便计算设计指标临界点的弯沉（已知p=0.7 MPa，双圆荷载，δ=10 cm）。

表6-2　算例6-5的结构和材料表［3］

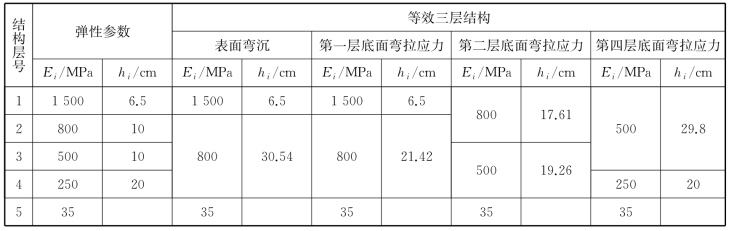
按照上面的准则，换算过程中，第一层（面层）的厚度和模量、路基的模量保持不变，第二、三、四层转换为E2=800 MPa的层次。由式（6-10）可得其厚度为：

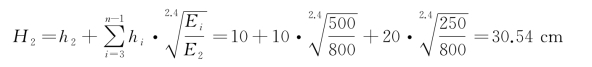
由此计算的路面弯沉为0.70 mm，采用计算机软件计算的弯沉为0.72 mm，可以看出是基本一致的。

在进行上层底面弯拉应力计算时，可将n层路面结构按照上层底面弯拉应力进行等效换算，其基本方法如图6-11所示。当要利用三层结构诺谟图求解n层结构中第j层层底面的弯拉应力时，保持第j层、第j+1层和土基的模量不变，将第j层以上的各层材料厚度按照式（6-11）换算成第j层材料厚度，第j+1层以下、土基以上各层材料按照式（6-12）换算成第j+1层，形成一个等效的三层结构［4-6］；该等效结构第一层层底面的弯拉应力与原结构第j层层底面的弯拉应力相等。

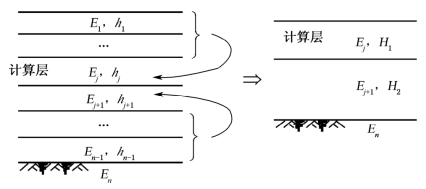
图6-11　等效上层底面弯拉应力的结构层换算

式中　H1——换算后的等效结构的第一层厚度；

H2——换算后的等效三层结构的第二层的厚度；

hi，Ei——分别为原n层结构第i层的厚度和模量；

hj，Ej，hj+1，Ej+1——分别为原n层路面结构中第j层与第j+1层的厚度和模量。

当要进行n层路面结构中邻近土基的层次（第n-1层）底面的弯拉应力计算时，路面结构等效换算的基本方法如图6-12所示。此时将第n-1层作为中层，保持第n-1层、第n-2层和土基的模量不变，将第n-2以上的各层按照式（6-13）换算成第n-2层，计算其等效厚度并与第n-2层厚度叠加，形成等效的三层结构［4-6］；该等效结构第二层层底面的弯拉应力与原结构第n-1层层底面的弯拉应力相等。

图6-12　等效中层底面弯拉应力的结构层换算

式中　H1——换算后的等效结构的第一层厚度；

hi，Ei——原n层结构第i层的厚度和模量；

hn-2，En-2——原n层路面结构中第n-2层的厚度和模量。

示例的计算过程可参见【例6-5】。