应力-应变性能铺面工程学

对于用作基层和垫层的无结合料碎（砾）石材料，由三轴试验所得到的应力-应变关系具有同黏性土不同的非线性特性，如图5-12所示。

因而，表征其应力-应变关系的回弹模量值Er随偏应力σd的增大而增大，也随侧限应力σ3的增大而增大，但侧限应力对其的影响常常要比对黏性土的影响大得多。

根据大量试验结果，对碎（砾）石材料，由三轴试验所得到的回弹模量值可用式（5-21）表示：

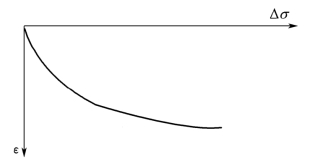
图5-12　颗粒材料的应力-应变关系曲线

式中　θ——主应力之和，kPa；三轴试验中，θ=σ1+2σ3=σd+3σ3；

k1，k3——同材料性质有关的系数，由试验确定。(www.xing528.com)

图5-13所示为某碎石集料的试验结果。由回归分析可得到，k1=3.77，k2=0.71。一般情况下，碎石集料的k1变动于7.00～15.70，k2变动于0.46～0.64。

图5-13　碎石集料的回弹模量Er随主应力之和θ变化的试验曲线

除了受应力状况的影响外，碎（砾）石材料的模量值同材料的级配、颗粒形状和密实度等因素有关，在100～700 MPa范围内变动。通常，密实度越高，模量值越大；颗粒棱角多者有较高的模量；当细料含量不多时，含水率的影响很小。

材料的泊松比取决于主应力比或偏应力σd与平均法向应力p（p=θ/3）的比值，随σd/p的增加而增加；设计计算时，可近似取用0.30～0.35。

设计路面结构时，碎（砾）石材料模量值的取用较为复杂。面层结构较厚时，传给粒料层的应力级位较小，碎（砾）石材料的应力-应变关系可近似看成线性。但当面层结构较薄时，必须考虑粒料层的上述非线性特性。碎（砾）石基（垫）层所能达到的密实度，依赖于其下面的支承结构的刚度，同时，由于非线性和缺乏抗拉能力，其模量值随路面结构层组合及其毗邻结构层的刚度而异，因此，不宜在应力-应变计算中简单地直接采用单独试验时得到的模量值，而可以按粒料层所受到的应力状况采用迭代的方法来确定相应的模量值。为了简单，通常可取为路基模量值的一定倍数，此倍数同粒料层的厚度和路基模量有关，大体上变动在1.5～7.5的范围内，一般情况下，采用2.5较合适［5］。

粒料的模量还与其含水率有关，含水率越大则其模量越小。当试验时粒料的含水率采用最佳含水率时，则所测得的模量一般小于路面结构中的数值，设计时应乘以湿度调整系数予以修正，详见本书8.4.4节。