路面温度场预测技术在铺面工程学中的应用

1.热传导方程法［6］

路面内的温度状况，可以采用热传导方程根据气象资料来计算。由大气进入路表面的热流，向路面结构内部传导；对于长度和宽度方向均尺度有限的路面结构来说，可以近似地认为路表面平面上各点受到的气候影响是一致的，故可将其假设为热流仅向路面结构深处传导的一维热传导。由于路面各结构层材料的导热性能相差不大，可以近似地将路面结构简化为均质半无限体。按此假设，路面的温度场可用均质半无限体的一维热传导方程来表示：

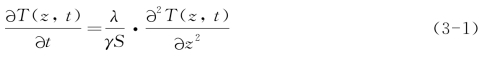
式中　T（z，t）——路面的温度场；

z——距表面深度，m；

t——时刻；

λ——路面材料的热传导系数，W/（m·℃）；

γ——路面材料的密度，kg/m3；

S——路面材料的热容量，J/（kg·℃）。

美国E.S.Barber假定路面结构为半无限体，且满足如下边界条件：

z→∞时，T（∞，t）≠∞

并把影响路面温度的两项主要气象变量——气温和太阳辐射，综合成一种当量的有效温度Te，假设它随时间呈正弦周期变化［7］：

式中　Tm——平均有效温度，℃；

式中　Ta——平均气温，℃；

R——辐射热使气温增高为有效气温的平均增量，℃；估计长波再辐射（有效辐射）的净损失平均约为1/3，则

式中　b——路面对辐射热的吸收能力，%，见表3-1；

Q——太阳的日辐射热，J/m2；

hc——考虑对流和再辐射的表面系数（对流系数），W/（m2·℃），可近似按式（3-5）计算：

式中　v——平均风速，km/h；

Tv——相对于平均有效温度的半波幅，℃，可近似按式（3-6）计算：

式中　TR——气温的日变化幅度，℃；

t——从温度周期起点算起的时间，h。

根据这些条件求解式（3-1），可得路面结构内的温度场为

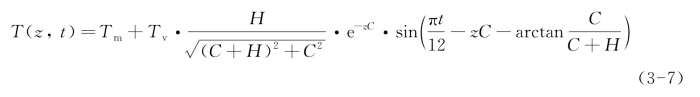
式中　H——对流系数与面层材料热传导率的比值，即H=hc/λ；

C——路面材料热特性综合参数：

根据式（3-7）、气象资料和路面材料的热特性参数，就可以确定单一路面层内的温度状况。

计算路表面最大温度时，以z=0代入式（3-7），并取正弦函数的最大值，可得：

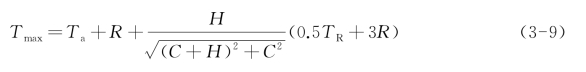
鉴于半无限体的假设，Barber公式主要适用于估算路面表面的温度变化。但由于面层以下各结构层的热传递性能的变化对面层上部的温度状况影响很小，此公式也可用于估算面层内接近面层范围内的温度状况。

除了Barber所用的方法外，也可以通过建立路面热平衡式，作为边界条件进行求解。对于多层路面结构，则可采用有限元方法或差分法求解。

【例3-1】某地某日的最高气温为27.9℃，最低气温为19℃，日辐射热为2 622.5 J/cm2。按照Barber方法估算沥青混合料路面下2 cm深度处的温度。

【解】沥青混合料的热特性参数按表3-1取为：b=95%，λ=1.214 W/（m·℃），S=921 J/（kg·℃）。沥青混合料的容重取为γ=2 240 kg/m3。当地平均风速为v=9.24 km/h。路面下2 cm处出现最高温度时，式（3-7）中的正弦函数必等于1，由此该式可写为：

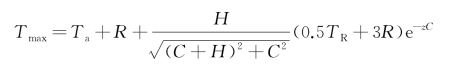
由题中给定的参数可得：

最后，Tmax=23.45+9.47+0.65（0.5×8.9+3×9.47）×0.85=51.08℃。

根据实测资料得知，最高温度出现在14：00左右。以此时刻作为最高温度出现时刻，可以推算出温度周期起点时刻，即由

代入上述有关数值，得t=7.77 h，温度周期起点时刻为14-7.77=6.23（6：13′48″即6点13分48秒）。

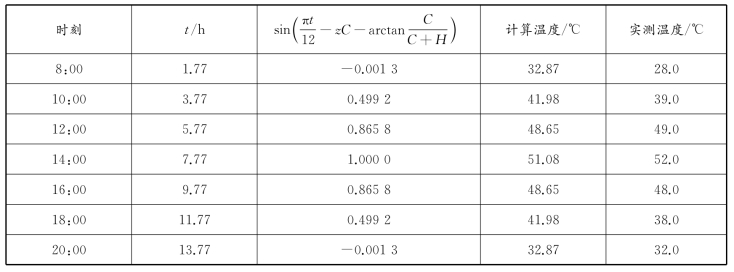
依据此起点时刻，由式（3-7）推算一天内不同时刻的温度，结果列于表3-2；表中还列出了实测的温度值。可以看出，最高值附近估算的温度同实测结果比较接近。不过，由于在Barber提出的模型中仅考虑了日辐射总量而并未考虑小时辐射量，以及影响参数众多，该模型的预估精度有限［1］。

表3-2　计算的路面温度与实测结果的对比

2.相关分析法

路面结构与大气之间的热交换以及路面有效辐射虽然对路面温度也有重要影响，但是目前还无法从气象部门获得这方面的资料。而路面与大气之间的热交换和路面有效辐射主要取决于气温的变化。因此，在路面温度场的预估模型中可以通过气温反映二者的影响。

风速是影响路面结构与大气之间对流热交换的另一个重要因素。但是在自然环境中，风速和风向时刻变化。即使对于同一路面结构，由于附近地形的差异，风速也会有所不同。因此，在预估模型中考虑风速的影响几乎是不可能的。

相对于气温和太阳辐射而言，云层状况、大气的相对湿度、降水等环境因素仅对特定天气状况下的路面温度场有一定影响，且与气温和太阳辐射之间具有一定的相关性。因此，这些因素的影响可以通过气温和太阳辐射部分体现出来。

综上所述，气温和太阳辐射是影响路面温度场的主要环境变量。在建立预估模型时，仅考虑气温和太阳辐射，而忽略其他因素的影响，既可以简化模型参数，减少输入参数数量，同时也可以达到较高的预测精度。

1）Superpave温度模型

1987年，美国启动了SHRP（Strategic Highway Research Program）计划，提出沥青及沥青混合料的性能按照气候分区评价的设想，要求沥青结合料必须在不同等级的最高和最低设计温度下满足性能要求。因此，了解路面在实际使用过程中所经受的极端温度条件就显得至关重要。所以，围绕路面的最高、最低温度，美国、加拿大开展了大量的研究。

SHRP报告［8，9］指出，在高温条件下，路表温度是由路表的热气流决定的。而路表热气流是由多方面的因素决定的，可用下式表示：

路表热气流=直接太阳辐射+热扩散±空气对流±热传导-路面体辐射

Superpave高温模型采用一年中温度最高的连续7天路面表面的最高温度（即温度最高的7天的平均温度值）作为沥青路面高温设计温度：

式中　Tsmax——路表最高温度，℃；(www.xing528.com)

Ta——最高气温，℃；

Lat——纬度，°。

路面某一深度处的最高温度可以通过式（3-11）由路表最高温度计算得到：

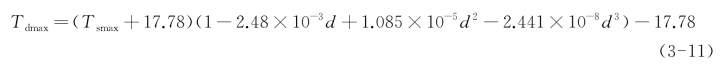
式中　Tdmax——路面特定深度处的最高温度，℃；

Tsmax——路表最高温度，℃；

d——距路表的深度，mm。

Superpave以路表下20 mm处的最高温度为路面的高温设计温度，由式（3-10）和式（3-11）可得：

式中　TMAXPVT——路面高温设计温度，℃；

Tairmax——最高气温，℃。

关于路面最低温度，Superpave研究认为冬季路面最低温度发生在路表处，因此，以路表最低温度为路面的低温设计温度。在建立路面低温设计温度模型时，可以依据的低温条件下的路面温度数据是十分有限的。由于缺少足够的数据，Superpave最终决定使用最为保守的估算方法——路表最低温度等于最低气温。由此Superpave的路面低温设计温度为

式中　TMINPVT——路面低温设计温度，℃；

Tsmin——路表最低温度，℃；

Tamin——最低气温，℃。

而路面特定深度处的最低温度可以由式（3-14）通过路表最低温度计算得到：

式中　Tdmin——路面特定深度处的最低温度，℃；

Tsmin——路表最低温度，℃；

d——距路表的深度，mm。

不过，加拿大的研究认为，冬季路表最低温度远远高于最低气温，并认为由式（3-14）得到的结果过于保守。

2）沥青路面温度场模型（同济模型）

本书3.2.2节中指出，相对于气温、太阳辐射等外界因素的变化，路面温度的变化具有滞后性（延迟性）和累积性的特点，如图3-10所示。延迟性是指气温、太阳辐射等外部因素对路面温度变化的作用并不立即显现，而是要过一段时间后才会显现。路面表面的延迟很小，可以忽略不计，而路面深处的延迟时间较长，离路表的距离越大，则延迟时间越长。累积特性是指路面目前的温度是之前一段时间内外部因素总影响的体现。

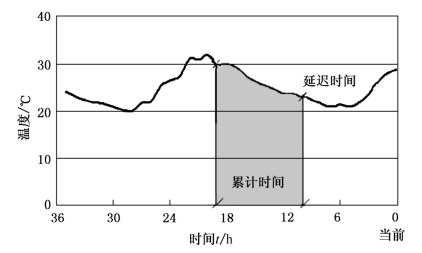
图3-10　路面温度变化的延迟性和累积性

由于路表温度的周期性变化和路面结构内部的热量交换，路面温度场沿深度方向的分布是十分复杂的。路面温度场在一天中不同时刻的典型分布如图3-11所示，图中散点表示不同时刻路面温度沿深度的分布，曲线是用三次多项式对路面温度沿深度方向的分布进行的拟合。研究表明，采用路面深度的三次多项式可以得到对路面温度场较为满意的拟合精度。

随着路面深度的增加，气温和太阳辐射对路面温度的影响程度逐渐减弱。在预估模型中可以引入气温和太阳辐射与路面深度的乘积项，以反映环境因素对于路面不同深度处温度的不同影响程度。

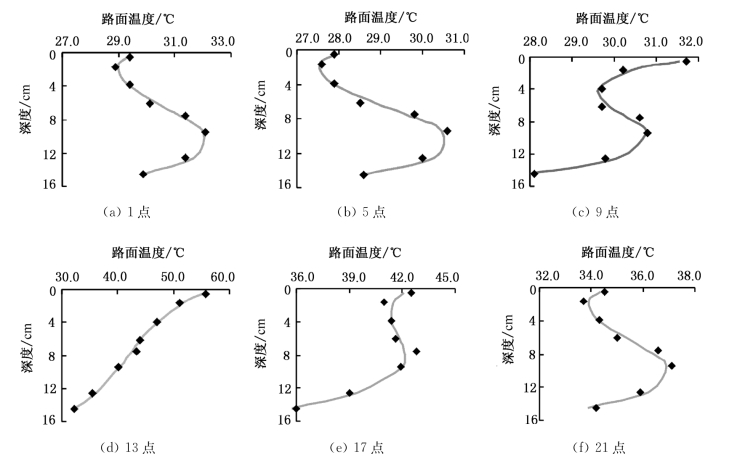
图3-11　沥青路面温度沿深度的典型分布状况

研究发现［5］，路面温度不仅受到每日周期性变化的各种环境因素的影响，还与处于路面结构下方的大地产生着持续的热量交换。而热量交换是由路面与大地之间的温度差异决定的，所以路面温度必然受到地温的影响。大地具有巨大的体积和热容量，相比各种环境因素而言，地温主要是由某些长期变化因素（如气候等）和外部环境影响滞后的累积所共同决定的，其变化过程缓慢而稳定。这就决定了地温对于路面温度的影响是一个长期且稳定的过程，在一定的时间段内其影响程度可以视为恒定，但就全年而言也是周期性变化的。因此，路面温度可以视为由两部分叠加而成的，即由长周期变化因素所决定的基准温度和由气候短期波动所决定的周期性变化的叠加。值得注意的是，长周期变化的基准温度在不同地区是不同的，且对路面深处温度的影响较大，对路表温度的影响较小。

因此，在预估模型中使用月平均温度Tm和月平均温度与深度的乘积Tm×d两项变量，以反映不同地区的地温对不同深度路面结构的影响差异［1，10-12］。

基于以上分析，可得预估模型如式（3-15）所示［12］：

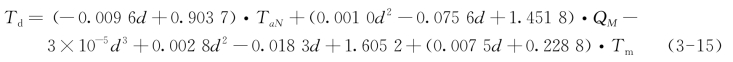
式中　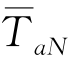——N小时内气温平均值，℃；

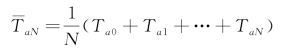
QM——M小时内太阳辐射总曝辐量，MJ/m2；

QM=（Q0+Q1+…+QM）

N——气温累积作用时间，小时；

M——太阳辐射累积时间，小时；

Tm——预估地区的当月历年月平均气温，℃；

d——路面深度，cm。

式（3-15）是根据多地不同深度的沥青路面温度实测数据和气象数据得到的结果。

对于水泥路面，20世纪70年代末和80年代进行了比较多的研究。同济大学、原上海市政工程研究所、空军后勤部工程设计局、原交通部重庆公路所以及原哈尔滨建筑工程学院等单位在北京、上海、广州、哈尔滨和重庆等地设置了10个水泥混凝土路面温度观测点，依据当地的气象资料和观测的数据，建立了相应的经验预估模型，如表3-3所列［13］。

表3-3　各温度观测点建立的路面温度预估关系式

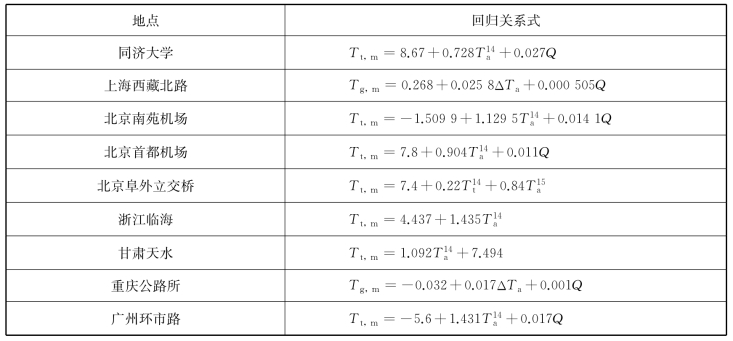
注：Tt，m为路面顶面最高温度（℃）；Tg，m为最大温度梯度（℃/cm）；Q为太阳日辐射量（Cal/cm2，1 Cal=4.186 8 J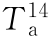）；为14：00时的气温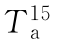（℃）；为15：00时的气温（℃）；ΔTa为日期温差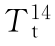（℃）；为14：00时的地温（℃）。

同济大学还采用太阳日辐射量、日最高气温和日温差作为气象因素变量，并选取面层标准厚度为22 cm时的最大温度梯度作为温度状况预估变量，在综合整理各温度观测点的测定数据，并将它们调整到基本相同的条件后，通过逐步回归分析，建立了二元和一元回归关系式［14］：

式中　Tg，m——最大温度梯度，℃/cm；

ΔTa——日温差，℃；

Q——太阳日辐射量，J/cm2。

设计时，为了便于考虑气候状况的影响，根据气候对路面温度的影响，全国被分成了多个区域，如表3-4和表3-5所列。

表3-4　按照高温考虑的温度区域划分

表3-5　按照低温考虑的温度区域划分