内力相关曲线计算方法

为了用本书方法和公式计算负弯矩作用下带补强板的腹板开洞组合梁的极限承载力，选取了3根编号为S1～S3的组合梁为计算对象，进行了比较分析。S1梁的洞口处未设置补强板，作为对比梁；S2、S3梁的洞口设置了不同尺寸的补强板，洞口中心线与钢梁形心轴重合，洞口位于负弯矩区。组合梁均为完全剪切连接设计，栓钉以等间距100 mm沿全梁均匀布置；混凝土翼板为C30，钢材均为Q235热轧H型钢，混凝土板中钢筋采用了HRB335级钢筋，配筋率0.8%，栓钉均采用ϕ19，长度为80 mm；材料属性采用第2章中试验得到的实测结果；各试件的几何尺寸以及基本参数分别见图7.16和表7.1。

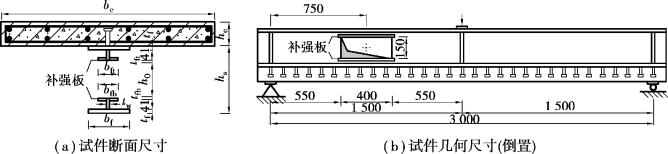
图7.16　负弯矩区带补强板的组合梁示意图

表7.1　带补强板的组合梁参数

根据本书提出的带补强措施的负弯矩区腹板开洞组合梁极限承载力计算方法对组合梁S1～S3进行计算，同时考虑洞口上方和下方截面的轴力平衡条件，得到对应的轴力-次弯矩相关曲线，如图7.17所示。

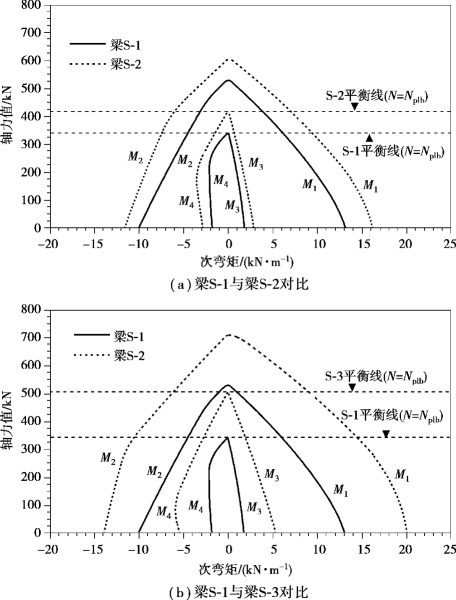
图7.17　不同补强板的负弯矩区腹板开洞组合梁轴力-次弯矩相关曲线(www.xing528.com)

从图7.17中可以得出如下结论：

①随着轴力的增加，洞口上方截面的次弯矩M1、M2和洞口下方截面的次弯矩M3、M4都逐渐减小，当轴力达到各自截面的最大塑性轴力时，对应的次弯矩为零；平衡线以下的部分为轴力平衡区域，即洞口上方、下方截面的轴力相互平衡，而平衡线以上的部分轴力不能平衡，只有平衡区内的次弯矩M1、M2是可以利用的；各平衡线所对应的轴力值是下方截面的最大塑性轴力Nplb。

②没有补强的组合梁S-1与洞口处设置了补强板的组合梁S-2、S-3相比，其次弯矩和轴力值均最小，组合梁S-2、S-3在设置补强板后次弯矩值和轴力均有很大提高；同时，设置补强板后满足轴力平衡的范围也明显扩大，使得次弯矩M1、M2的有效利用区域增加，原因是补强板提高了洞口下方截面的最大塑性轴力Nplb；可见在洞口处设置水平补强板使得次弯矩明显提高，补强板面积越大，次弯矩增加越多。

计算得到了组合梁S1～S3的轴力-剪力相关曲线，如图7.18所示。通过比较可以看出：组合梁S-2、S-3与组合梁S-1相比，洞口上方和下方截面的抗剪承载力（Vb、Vt）都明显增大，由于组合梁S-3的补强板面积最大，对应的剪力增加幅度也最多。同时发现，洞口上方截面的剪力Vt远大于下方截面的剪力Vb，再次说明了混凝土翼板对负弯矩作用下的腹板开洞组合梁的竖向抗剪承载力有很大贡献。

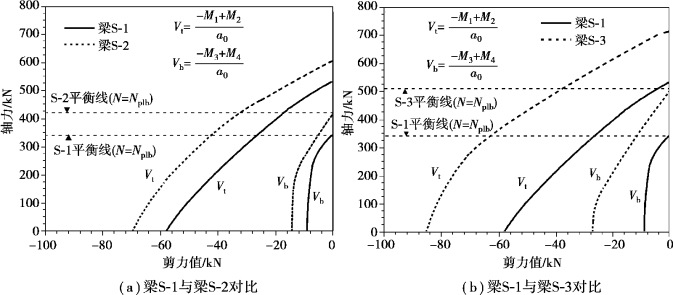
图7.18　不同补强板的负弯矩区腹板开洞组合梁轴力-剪力相关曲线

在计算得到的轴力-次弯矩相关曲线和轴力-剪力相关曲线基础上，给出相应的轴力值，就可以求得对应截面的总弯矩Mg和总剪力Vg，其中，总弯矩由主弯矩和次弯矩叠加得到，即/2；总剪力由洞口上方截面剪力Vt和下方截面剪力Vb叠加得到，即Vg=（Vt+Vb）。