内力曲线分析应用-混凝土组合梁腹板开洞试验及理论研究

选择第2章中的试验梁SCB-2为例，分析其截面上的内力相互关系，计算负弯矩作用下的腹板开洞组合梁的极限承载力。试件示意图及截面尺寸如图5.15所示，材料属性采用试验得到的实测结果；组合梁混凝土翼板的有效宽度，按我国《钢结构设计标准》（GB 50017—2017）确定。

图5.15　组合梁试件示意图与截面尺寸（SCB-2）

计算得到了负弯矩作用下组合梁SCB-2洞口区域截面的轴力-次弯矩相关曲线和轴力-剪力相关曲线如图5.16、图5.17所示。从图5.16中可以看出：洞口上方截面的次弯矩M1、M2以及洞口下方截面的次弯矩M3、M4都随轴力的增加而逐渐减小；当轴力达到各自截面的最大塑性轴力时，对应的次弯矩为零。由于洞口上方、下方截面内的轴力必须相等才能平衡，即图5.16中平衡线以下的部分为平衡区域，该区域内的洞口上、下方截面的轴力可以相互平衡；而平衡线以上的部分则超越了洞口下方截面的最大轴力范围，该区域（阴影部分）不再满足轴力平衡条件，区域内的次弯矩M1、M2是不能被利用的。各平衡线所对应的轴力值就是洞口下方截面的最大塑性轴力Nplb。在平衡区域内给定一个轴力值N，就可以得到对应的次弯矩值，将次弯矩Mi和主弯矩Mp叠加可以得到洞口处的总弯矩。

图5.16　负弯矩区洞口轴力-次弯矩相关曲线

从图5.17中可以看出：洞口上方、下方截面的剪力值均随着轴力的增加而下降，说明洞口截面上的轴向力对抗剪承载力是不利的，同时发现，洞口上方截面的剪力Vt远大于下方截面的剪力Vb，说明了混凝土板对负弯矩区腹板开洞组合梁的竖向抗剪承载力有很大的贡献。在平衡区域内，将洞口上方截面剪力Vt和下方截面剪力Vb叠加可以得到洞口处的总剪力Vg。(www.xing528.com)

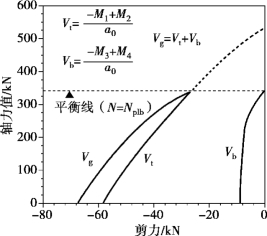
图5.17　负弯矩区洞口轴力-剪力相关曲线

为了便于实际应用，制作出负弯矩区洞口处的轴力-剪力-弯矩相关曲线图，如图5.18所示，通过该图可以更为直观地得到洞口处的抗弯和抗剪承载力。

从图5.18中可以看出：轴力-剪力-弯矩相关曲线是由极限状态下可能出现的各种内力组合构成的，曲线上的每一个点代表着一种内力组合情况，给定了一个轴力N，可以求出唯一对应的总剪力Vg和总弯矩Mg，为了简化计算，洞口区总弯矩Mg取为与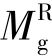次的平均值，即Mg=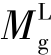（+）/2。在选择轴力N时，需要考虑多个受力情况，如洞口上方截面的拉力（忽略混凝土受拉）、洞口下方截面压力以及洞口区的抗剪连接件栓钉所承担的纵向剪力等，通过对比选择起控制作用的轴力。图5.18中的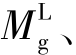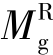分别为洞口左端、右端总弯矩，Mp为主弯矩，其中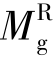和Mp均为负值，则有一部分为正值，且的绝对值大于，这是由于洞口左端截面的部分材料强度被正的次弯矩M1、M3所消耗，而右端截面的材料强度则全部由负的次弯矩M1、M3和主弯矩Mp消耗。

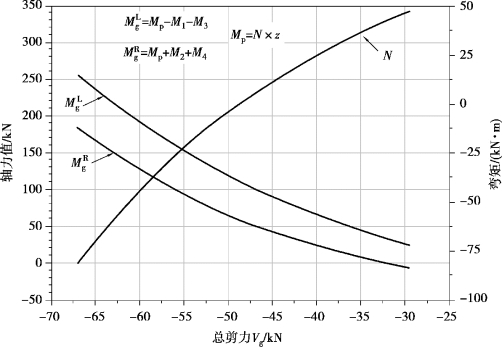
图5.18　负弯矩区洞口处的轴力-剪力-弯矩相关曲线