1)洞口角点3的次弯矩M3j
负弯矩作用下洞口角点3截面的应力分布及中和轴NA的变化情况如图5.10所示,该截面的轴力为负值,次弯矩为正值,截面上部受压下部受拉,随着轴力的增加中和轴NA只能从面积平分轴开始向下移动,由于面积平分轴只能出现在钢梁翼缘内,所以中和轴NA只经过一个区域,即NA在钢梁翼缘内[图5.10(a)、(b)],次弯矩函数M3j仅由一段函数组成。
从图5.10中可以看出:当轴力为零,次弯矩达到最大值时,面积平分轴FA与中和轴NA重合[图5.10(a)];随着轴力的增加,NA依次经过轴力和弯矩共同存在的区域[图5.10(b)];当轴力达到最大值时,相应的次弯矩为零[图5.10(c)]。
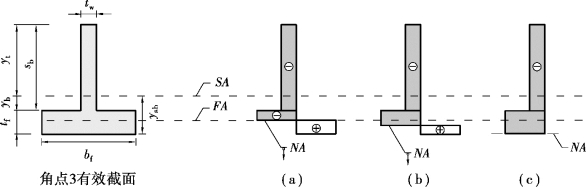
图5.10 负弯矩区角点3截面上的应力分布及中和轴的变化范围
分析情况:中和轴NA位于钢梁下翼缘内
随着轴力的增加,中和轴从面积平分轴开始向下移动,中和轴的移动范围在钢梁下翼缘内,如图5.11所示。此时满足条件:
![]()
①确定角点3截面的形心轴位置:
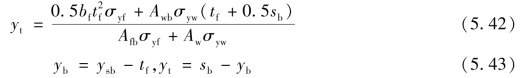
②考虑到中和轴位于钢梁下翼缘内,为了满足换算应力图中面积平分轴与实际截面的面积平分轴位置相同,将洞口上方、下方钢梁截面的最大塑性轴力差换算成钢梁翼缘的折算高度:

![]()
其中,Nplb为洞口下方钢梁截面的最大塑性轴力。
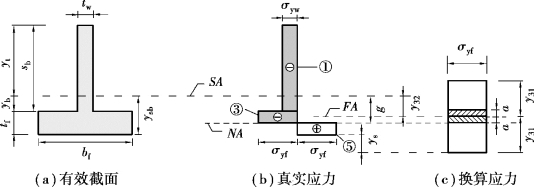
图5.11 中和轴NA在钢梁下翼缘时角点3截面上的应力分布图
③确定换算应力图中面积平分轴的位置:
![]()
④确定形心轴SA到面积平分轴FA的距离:
![]()
⑤确定洞口上方截面的无量纲轴力nb以及折算高度a:
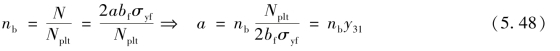
⑥确定形心轴SA到中和轴NA的距离:
![]()
⑦将真实应力图中①~③部分的合力对形心轴SA取矩可以得到次弯矩函数M3j的第一段函数式M31:
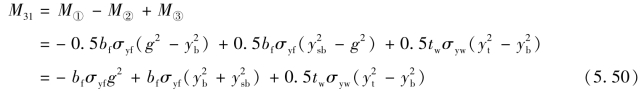
将式(5.49)代入式(5.50)可以得到:
![]()
简化后可以得到关于nb的函数式:
![]()
式中:
![]()
2)洞口角点4的次弯矩M4j
负弯矩作用下洞口角点4截面的应力分布及中和轴NA的变化情况如图5.12所示,该截面的轴力和次弯矩均为负值,截面上部受拉下部受压,随着轴力的增加中和轴NA只能从面积平分轴开始向上移动,由于面积平分轴只能出现在钢梁翼缘内,所以中和轴NA可以经过两个区域,即NA在钢梁翼缘内[图5.12(a)、(b)],NA在钢腹板内[图5.12(c)、(d)],根据中和轴NA位置的不同,次弯矩函数M4j由两段函数组成。
从图5.12中可以看出:当轴力为零,次弯矩达到最大值时,面积平分轴FA与中和轴NA重合[图5.12(a)];随着轴力的增加,NA依次经过轴力和弯矩共同存在的区域[图5.12(b)、(c)];当轴力达到最大值时,相应的次弯矩为零[图5.12(d)]。
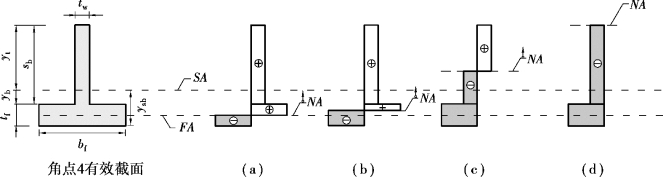
图5.12 负弯矩区角点4截面上的应力分布及中和轴的变化范围
分析情况(一):中和轴NA位于钢梁下翼缘内
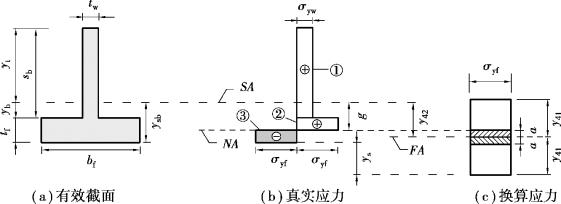
随着轴力的增加,中和轴从面积平分轴开始向上移动,中和轴的移动范围在钢梁下翼缘内,如图5.13所示。此时满足条件:
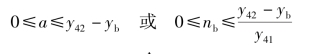
 (https://www.xing528.com)
(https://www.xing528.com)
图5.13 中和轴NA在钢梁下翼缘时角点4截面上的应力分布图
①为了满足换算应力图中的面积平分轴与实际截面的面积平分轴位置相同,将洞口上方、下方截面的最大塑性轴力差换算成钢梁翼缘的折算高度:

②确定换算应力图中面积平分轴FA的位置:

③确定形心轴SA到面积平分轴FA的距离:
![]()
④确定洞口上方截面的无量纲轴力nb以及折算高度a:
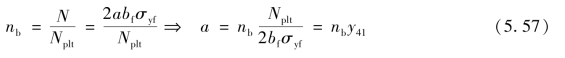
⑤确定形心轴SA到中和轴NA的距离:
![]()
⑥将真实应力图中①~③部分的合力对形心轴SA取矩可以得到次弯矩函数M4j的第一段函数式M41:
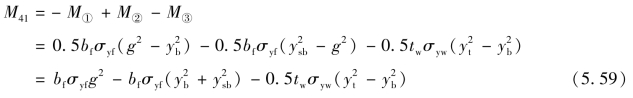
将式(5.58)代入式(5.59)可以得到:
![]()
简化后可以得到关于nb的函数式:
![]()
式中:
![]()
分析情况(二):中和轴NA位于钢梁腹板内
随着轴力的增加,中和轴继续向上移动,中和轴的移动范围由钢梁下翼缘顶部移动到钢梁腹板内,如图5.14所示。此时满足条件:
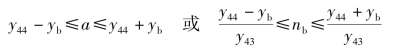
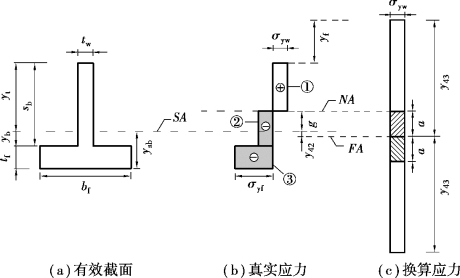
图5.14 中和轴NA在钢梁腹板时角点4截面上的应力分布图
①为了满足换算应力图中的面积平分轴与实际截面的面积平分轴位置相同,将洞口上方、下方截面的最大塑性轴力差换算成钢梁翼缘的折算高度:

②确定换算应力图中面积平分轴FA的位置:

③确定形心轴SA到面积平分轴FA的距离:
![]()
④确定洞口上方截面的无量纲轴力nb以及折算高度a:
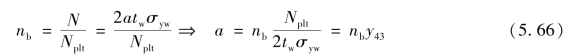
⑤确定形心轴SA到中和轴NA的距离:
![]()
⑥将真实应力图中①~③部分的合力对形心轴SA取矩可以得到次弯矩函数M4j的第二段函数式M42:
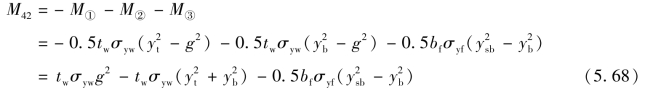
将式(5.67)代入式(5.68)可以得到:
![]()
简化后可以得到关于nb的函数式:
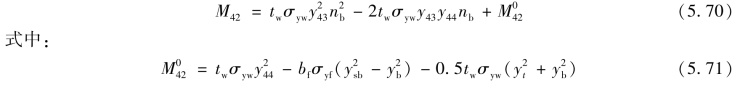
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




