负弯矩区钢-混凝土组合梁腹板开洞试验及理论研究计算方法

使用空腹桁架模型进行计算分析时，洞口区域的内力为3次超静定，多余未知量有洞口上方或洞口下方截面内的轴力、剪力和次弯矩，这3个内力共同消耗截面材料的强度，因此需要建立截面的轴力-弯矩-剪力相关关系（N-M-V关系曲线）以找出内力之间的耦联关系。在洞口的4个角部各有一个截面，每一个截面有自己的N-M-V相关关系，这些相关关系又可以通过建立次弯矩函数来反映，由此可以得到4个次弯矩函数：M1（Nt，Vt）、M2（Nt，Vt）、M3（Nb，Vb）、M4（Nb，Vb）。根据弯矩平衡条件可得：

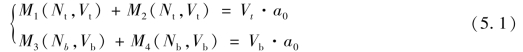
式（5.1）中每个方程各有Nt、Vt和Nb、Vb两个未知量，根据洞口上方截面和下方截面的轴力平衡条件，可得：

将式（5.2）带入式（5.1）中，可以减少一个未知量，式（5.1）可写为：

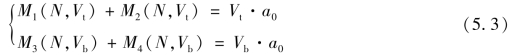
式（5.3）中的两个方程共含有3个未知量，通常是无法求解的，但是如果给3个未知量中的某个未知量一个定值，便可求出其余两个未知量。本书赋予洞口下方截面的剪力Vb不同的值，就能求出N和Vt，计算流程如图5.2所示，计算前还需要知道Vb的最大值，即确定Vb的取值范围（0～Vb，max）。

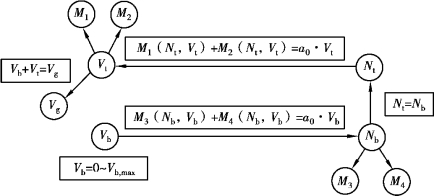
图5.2　计算流程

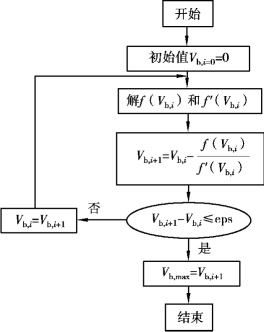
在确定Vb的最大值Vb，max时，必须考虑整个结构的轴力平衡条件，由于洞口下方截面的面积较小，其承载力小于洞口上方截面，因此下方截面的承载力起控制作用，Vb，max的确定过程如图5.3所示，计算过程中利用式（5.3）中的第二式进行迭代求解。

(www.xing528.com)

图5.3　确定Vb，max的流程

从图5.2的计算流程图中看出，当洞口下方截面的剪力Vb确定后，带入式（5.3）就可以求出对应的N和Vt，将求得的轴力和剪力值代入式（5.1）就可以得到洞口4个角点处的次弯矩函数。

当洞口上方、下方截面的内力全部求出后，根据全截面受力平衡条件，如图5.1所示，可以得到洞口处的总弯矩Mg和总剪力Vg：

式中　——洞口左端和右端的总弯矩；

　　　Mp——主弯矩，Mp=N·z；

　　　N——洞口区轴力；

　　　z——洞口上方、下方截面形心轴之间的距离；

　　　Mg——洞口区的总弯矩；

　　　Vg——洞口区总剪力。