试验结果与有限元结果对比：取得的成果

1）混凝土板裂缝

通过对负弯矩作用下腹板开洞组合梁的试验，可以将混凝土裂缝发展过程分为以下几个阶段：

当荷载达到0.25Pu时，靠近加载点的洞口右侧的混凝土板下表面开始出现微小的横向裂缝，随着荷载增加，裂缝缓慢发展；当荷载达到0.58Pu时，洞口区域上方混凝土板的横向和纵向裂缝也显著增加；当荷载达到0.75Pu时，右侧洞口上部混凝土板开始出现鼓起，横向和纵向裂缝开始贯通，宽度也有所增加；当荷载达到0.9Pu时，裂缝发展充分，宽度明显；荷载达到Pu时，靠近洞口区域的混凝土板出现明显断裂，详见试验部分内容。

通过ANSYS模拟计算得到了组合梁试件的混凝土板底裂缝情况，如图3.21所示。从图中结果可以看出：混凝土板裂缝在洞口区段最为密集，在洞口左、右两端截面上方的混凝土裂缝最多，其次在加载点处（跨中）的混凝土板也出现了较多裂缝，有限元模拟的裂缝情况与试验情况比较相似。

图3.21　有限元模拟混凝土板底裂缝（一半模型）

2）破坏形态与变形

图3.22所示为负弯矩区腹板开洞组合梁的试验破坏与有限元结果对比图。在本次试验中，5根开洞组合梁试件在弯剪共同作用下，洞口区不仅发生了剪切变形，角部还出现了塑性铰，从整体上看，开洞试件的破坏形态属于空腹破坏。

以试件SCB-2为例，当试件处于弹性阶段时，钢梁全截面处于弹性应变状态，在跨中和洞口右侧的混凝土板底部出现少量微小的横向裂缝，发展速度缓慢；当洞口区域的腹板或下翼缘开始出现屈服时，试件就进入了弹塑性阶段，此阶段中，洞口4个角处相继发生变形屈服，混凝土板与钢梁交界面出现明显的滑移，裂缝发展迅速，随着荷载的增加，钢梁洞口处腹板和下翼缘的最大应变超过钢材屈服应变，整个组合梁刚度明显下降，试件整体变形明显；在试件的破坏阶段，洞口区域4个角处的钢梁全截面屈服，出现塑性铰，有的角部被明显拉裂，有的角部受到挤压，洞口出现了很大的剪切变形；混凝土板发生剪切破坏，断裂部位在洞口两侧，栓钉在较大的掀起力作用下被拨出一段，如图3.22（a）、（b）所示。

图3.22　试验现象与有限元结果对比

从有限元模拟计算得到的结果[图3.22（c）、（d）]看出，洞口区域4个角部处的腹板全截面屈服，出现塑性铰，洞口发生了较大的剪切变形，角部有拉裂和挤压，混凝土板与钢梁在交界面上出现了相对掀起，即栓钉拔脱的现象，通过对比发现有限元模拟计算得到的破坏形态与试验现象类似，说明有限元可以很好地模拟负弯矩区腹板开洞组合梁的受力过程。

3）荷载-挠度曲线对比

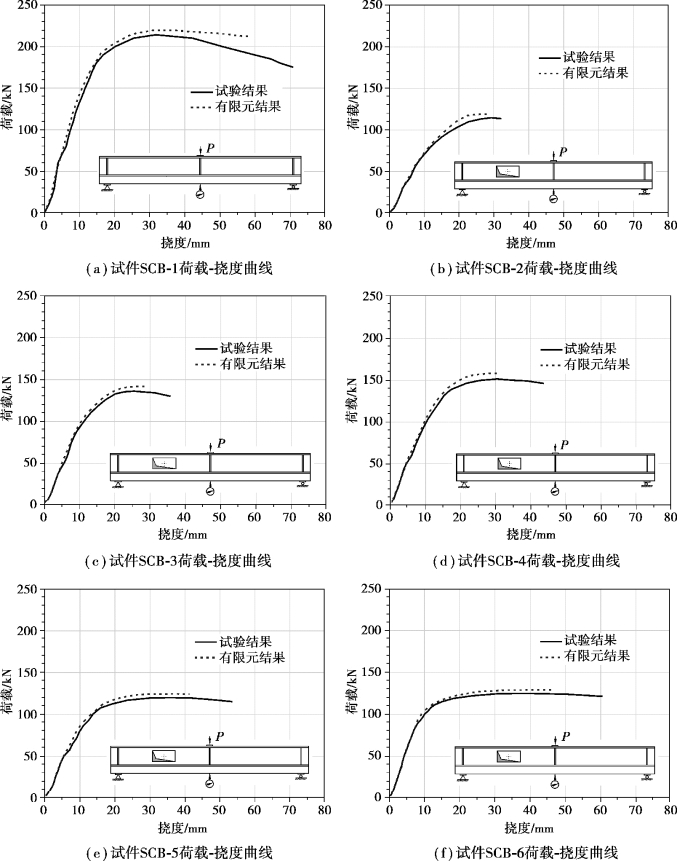
试验和有限元模拟计算所得到的全部试件的荷载-挠度曲线对比如图3.23所示。

通过对比可以看出：负弯矩作用下组合梁试件的有限元结果和试验结果在弹性阶段和弹塑性阶段是比较吻合的，所得到的极限荷载相差不大，但是在破坏阶段的最大挠度值比试验结果要小一些，原因首先是在负弯矩和洞口等不利因素下混凝土开裂较多造成了收敛困难，此外ANSYS在计算中采用了Newton-Raphson的迭代算法，难以计算出曲线下降段。Newton-Raphson的实质是用一系列荷载值[式（3.19）]和非线性方程[式（3.20）]进行联立求解。

求解过程相当于用式（3.19）表示的一组水平直线和曲线相交，同时通过得到的这些交点来定义整个求解的路径。一旦曲线上出现极值点时，求解路径在极值点处就难以通过，即使经过调整可以通过极值点，也不是正确的寻找范围，此时即使找到了，其误差也会很大，因为直线P=const与曲线的切线已经接近平行，所以，当Newton-Raphson法在遇到极值点时，相应的求解过程难以继续进行。

(www.xing528.com)

图3.23　组合梁试件荷载-挠度曲线

4）极限承载力对比

为了验证有限元方法得到的试件极限承载力的准确性，我们对试件进行了非线性有限元模拟计算，对应的6根组合梁试件极限承载力试验与有限元结果对比见表3.6，图3.24所示为各组合梁试件极限承载力的试验与有限元结果的比值分布。从结果中可以看出：试验得到的极限承载力与有限元结果对比较好，误差在7%以内，可以满足工程精度要求，从而验证了有限元方法的准确性。

表3.6　组合梁极限承载力试验与有限元结果对比

注：a0为洞口宽度，h0为洞口高度；bc为混凝土板宽度，hc为混凝土板高度。

图3.24　试件极限承载力有限元与试验结果比值分布

图3.25所示为负弯矩作用下腹板开洞组合梁在板厚和配筋率两参数变化下极限承载力对比柱状图。从图中可以看出：有限元方法可以很好地模拟混凝土板厚和配筋率两个参数变化时开洞组合梁试件的极限承载力，这就为使用有限元方法分析更多变化参数对负弯矩作用下的腹板开洞组合梁受力性能提供了可靠的参考。

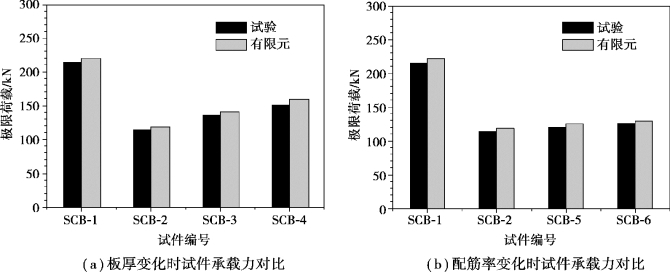
图3.25　参数变化下组合梁试件极限承载力有限元与试验结果对比

5）洞口区剪力分布

在ANSYS后处理中，不能直接得到3D实体单元的截面内力，为了获得所需要的截面内力要采用一定的方法。获取3D实体单元内力的方法主要有3种：截面分块积分法、面操作法以及单元节点力求和法。其中截面分块积分法是将截面分为很窄的条状，用路径获得每条长度方向的应力，再通过路径求得每一条的合力，各条合力汇总即为截面上的内力；面操作法通过映射应力到所定义的面上，对面上应力进行积分得到截面上的内力。为了较为精确地计算组合梁洞口区截面上的内力，可采用单元节点力求和法，该方法通过选择节点和单元，再对单元节点力求和即可得到对应截面的内力，此方法要求所求内力的截面为一列单元的边界，也就是截面不能穿过单元，因此在有限元建模过程中要提前设定好需要计算内力的截面，使其单元边界能够满足单元节点力求和法的要求。

表3.7为负弯矩作用下腹板开洞组合梁洞口区截面上混凝土板和钢梁的剪力承担值，同时列出了试验结果与有限元结果。可以看出：试验值与有限元计算结果吻合良好，影响误差的主要因素有：应变片的数量；应变片的测量误差；主应变增量比β的取值（见2.4节）等。

表3.7　负弯矩作用下洞口各部分截面承担剪力对比

注：Vc为混凝土板剪力；Vst为钢梁剪力；Vs为洞口上钢梁截面剪力；Vb为洞口下钢梁截面剪力。