无洞组合梁弹性分析及试验研究

《钢结构设计标准》（GB 50017—2017）采用了换算截面法计算组合梁在负弯矩作用下的刚度，计算时不考虑混凝土的抗拉作用，仅考虑钢筋和钢梁构成的组合截面，该方法忽略了混凝土板与钢梁之间的滑移，但相关试验和理论结果[48，55，115，116]表明，即使按完全剪切连接设计的组合梁，剪切连接件在水平剪力作用下也会发生变形，不存在无滑移的完全剪切连接状态。

1）负弯矩区组合梁弹性受力特性

对处于弹性工作阶段的负弯矩作用下的钢-混凝土组合梁，在考虑滑移效应影响时可以近似地将组合梁作为弹性体考虑，并有以下基本假设：

①钢梁与混凝土交界面上的相对滑移与水平剪力成正比。

②抗剪连接件沿梁长均匀布置，水平剪力沿梁长连续分布。

③混凝土翼板与钢梁具有相同的曲率，都符合平截面假定。

以跨中作用反向集中荷载的简支组合梁为例，坐标原点O位于跨中截面形心轴处，负弯矩作用下考虑滑移效应的组合梁变形微段模型如图3.10所示。

图3.10　负弯矩作用下组合梁微段变形模型

2）弹性理论与有限元结果对比

文献给出了负弯矩作用下考虑滑移效应的组合梁挠度计算公式，见式（3.17）。

式中　δf——按照换算截面法计算得到的弹性挠度；

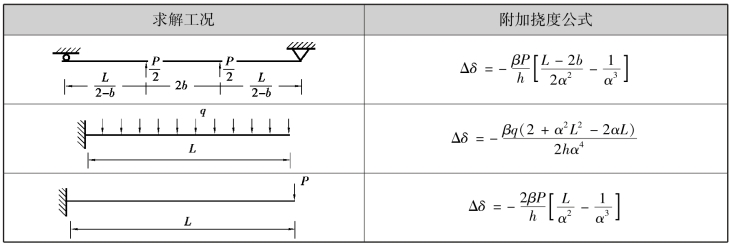
　　　Δδ——考虑滑移效应时的附加挠度，对于不同荷载工况下的附加挠度简化计算公式见表3.2。

表3.2　附加挠度公式

续表

注，d为栓钉间距，E为钢筋和钢梁的弹性模量，Is为钢梁的截面惯性矩，Ar，As分别为钢筋和钢梁的面积。

对于负弯矩作用下钢-混凝土组合梁界面滑移值的理论算法，根据文献，可以得到集中荷载作用下的滑移计算，见式（3.18），对应工况如图3.11所示。

(www.xing528.com)

式中，，d为栓钉间距，E为钢筋和钢梁的弹性模量，Is为钢梁的截面惯性矩，Ar，As分别为钢筋和钢梁的面积。

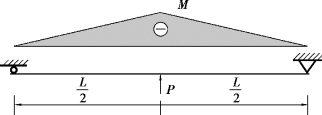
图3.11　组合梁负弯矩工况

为了研究负弯矩作用下组合梁在弹性阶段的受力性能，设计了4根栓钉间距不同的反向加载简支组合梁试件，对试件进行有限元计算分析，将有限元结果与上述理论计算方法得到的结果进行了对比。

4根组合梁试件编号为SC-1～SC-4，混凝土强度等级C30，钢材等级为Q235B，栓钉采用ϕ19，长度80 mm，按等间距沿梁长均匀布置，配置12根通长ϕ12钢筋，试件简图及尺寸如图3.12所示，试件设计参数见表3.3。

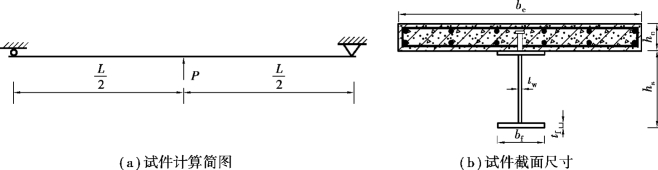
图3.12　试件示意图

表3.3　组合梁试件设计参数

通过有限元计算得到了负弯矩作用下组合梁挠度沿梁长的分布曲线，如图3.13所示，可以看出：各组合梁试件的最大挠度都出现在跨中位置，对栓钉间距最大的试件SC-1，其挠度值最大，随着栓钉间距的减小，组合梁试件的挠度依次降低，说明挠度随着连接程度的提高而减小，抗剪连接程度对组合梁的挠度影响是比较大的。

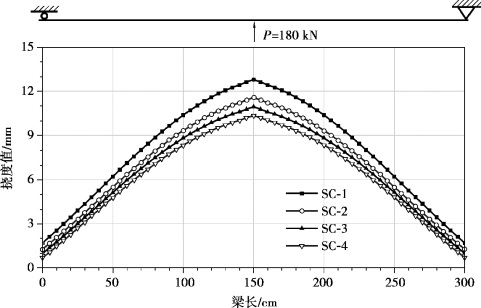
图3.13　负弯矩区组合梁挠度分布（ANSYS计算结果）

通过理论式（3.17）计算得到了组合梁试件的跨中挠度理论值，并与有限元结果进行了比较，见表3.4。计算结果表明：理论计算结果与有限元结果比较吻合，误差在10%内。

表3.4　挠度理论值与有限元结果对比

通过理论式（3.11）计算得到的各试件滑移值及其有限元结果，如图3.14所示。

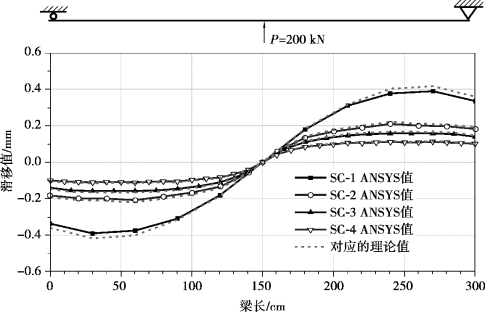
图3.14　负弯矩区组合梁滑移分布

从结果中可以看出：各组合梁试件的连接程度不同，但其滑移分布规律基本相似，滑移沿跨中基本为对称分布，最大值均出现在组合梁两端，跨中的滑移值为零；随着连接程度的降低，滑移值依次增加，连接程度越大滑移分布曲线越平缓，说明栓钉间距（连接件数量）对负弯矩作用下的组合梁滑移有较大的影响。