【摘要】:求解非线性问题的方法主要包括:全量法、增量法、初应变法和初应力法。计算结构非线性问题的实质,最终可以归结为求解非线性有限元方程的问题。使用ANSYS软件进行分析时,对于非线性方程的计算一般采用的是全量法中的Newton-Raphson算法,该方法是采用线性方法来求解非线性方程,对应的非线性代数方程见式(3.9)。图3.8NR法一维线性逼近
结构非线性问题包括材料非线性、几何非线性和状态非线性3类。求解非线性问题的方法主要包括:全量法、增量法、初应变法和初应力法。全量法包括Newton-Raphson法、修正的Newton-Raphson法和拟Newton-Raphson法;增量法包括增量加载法、线性加载法和联合求解法;初应力法和初应变法又包括全量迭代法、增量迭代法和增全混合迭代法。计算结构非线性问题的实质,最终可以归结为求解非线性有限元方程的问题。
使用ANSYS软件进行分析时,对于非线性方程的计算一般采用的是全量法中的Newton-Raphson算法,该方法是采用线性方法来求解非线性方程,对应的非线性代数方程见式(3.9)。
![]()
Newton-Raphson算法使用泰勒展开方法构造了线性逼近数列,如对于具有一阶导数的连续函数ϕ,在u(i)已知的情况下,在u(i)处作一阶泰勒展开,可以得到近似公式如下:
![]()
式中 ϕ(i)——u(i)处的不平衡力;
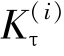 为u(i)处的切线刚度矩阵,其计算公式见式(3.11)。
为u(i)处的切线刚度矩阵,其计算公式见式(3.11)。
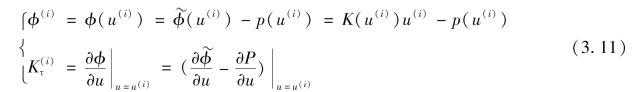 (https://www.xing528.com)
(https://www.xing528.com)
根据式(3.10),在满足不平衡力为零的条件下,求得新的逼近值u(i+1)为:
![]()
构造线性逼近数列的公式如下:

当式(3.13)退化为一维情况时,对应的线性逼近过程如图3.8所示。
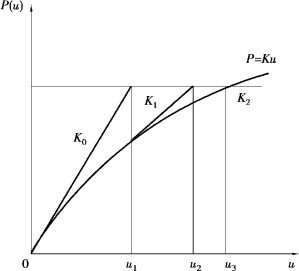
图3.8 NR法一维线性逼近
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




