【摘要】:根据Mises屈服条件,当等效应力σeq小于钢材的屈服强度fy时,材料处于弹性阶段;当等效应力σeq大于或等于钢材的屈服强度fy时,材料处于塑性阶段。根据应变数据,利用式(2.3)和图2.21可以求出β,将β代入式(2.7)就可以得到两个主应力;再根据应力圆,用式(2.8)求出塑性阶段的剪应力。图2.23钢梁与混凝土翼板的剪力计算流程
根据Mises屈服条件,当等效应力σeq小于钢材的屈服强度fy时,材料处于弹性阶段;当等效应力σeq大于或等于钢材的屈服强度fy时,材料处于塑性阶段。为了求得等效应力σeq,首先由应变数据求出主应力σ1,σ2,见式(2.4):
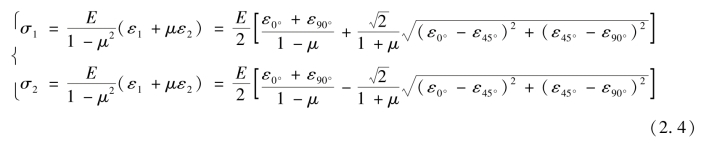
再由式(2.5)就能求出等效应力σeq:
![]()
1)弹性应力计算
当材料处于弹性阶段时,应力-应变曲线服从胡克定律(Hooke’s law),可以根据应变数据直接求出不同荷载阶段的应力值,如式(2.6)所示:

2)塑性应力计算
由于塑性阶段的应力-应变曲线不存在一一对应的关系,对于塑性阶段的应力计算相对困难,本书采用塑性流体理论得到的分离组合梁混凝土板和钢梁剪力的计算方法。
材料在塑性状态下,两个主应变的增量比β=Δε1/Δε2近似地趋于一个常量。根据应变数据,利用式(2.3)和图2.21可以求出β,将β代入式(2.7)就可以得到两个主应力;再根据应力圆(图2.22),用式(2.8)求出塑性阶段的剪应力。(https://www.xing528.com)

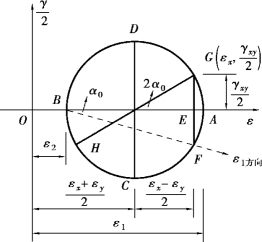
图2.21 应变圆
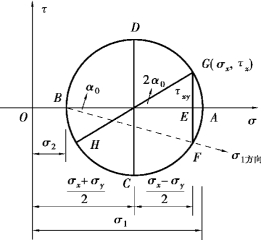
图2.22 应力圆
求出剪应力值τxy,就可以得到钢梁部分的剪力值Vs,这时由总剪力V减去Vs,即可得到混凝土板承担的剪力值Vc:Vc=V-Vs。
以上述理论方法为基础,可以计算出负弯矩区腹板开洞组合梁钢梁和混凝土板各自承担的剪力,根据计算步骤列出对应的计算流程图,如图2.23所示,按流程图可以方便地使用计算机编程进行计算。
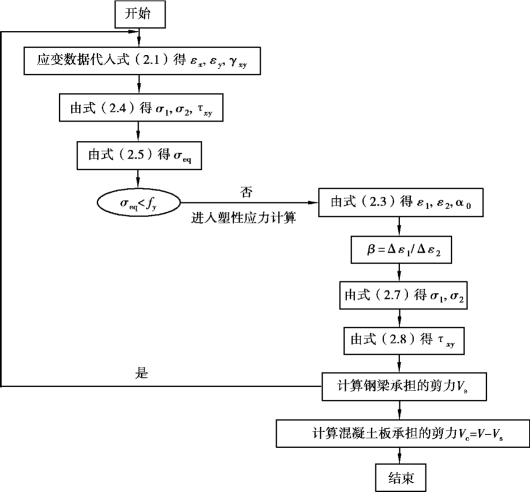
图2.23 钢梁与混凝土翼板的剪力计算流程
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




