截面设计校核规范-高层混凝土结构

《高层建筑混凝土结构技术规程》规定：

9.1.6 核心筒或内筒中剪力墙截面形状宜简单；截面形状复杂的墙体可按应力进行截面设计校核。

【例5.2.1】 圆形筒中筒结构底层窗间墙的应力计算

条件：某40层、高150m的圆形筒中筒结构如前图5.1.2所示。承受三角形分布的风荷载，顶部的风荷载标准值为60.8kN/m，设风力全部由外筒墙抵抗。外筒外径为32m、底层筒壁厚0.3m，窗洞面积为外筒面积的一半。外筒墙底部承受由竖向力形成的最大压应力设计值为11N/mm²。

要求：筒底窗间墙的应力设计值。

答案：

（1）外筒的截面惯性矩I外径D=32m，内径d=31.4m，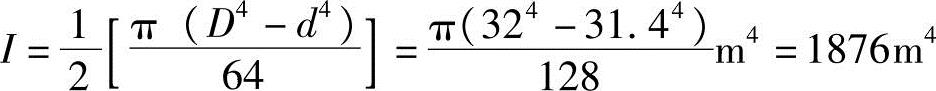

（2）风荷载产生的底部最大压应力标准值结构底层总弯矩。风荷载产生的最大压应力。

（3）风荷载和垂直荷载组合后，筒底窗间墙的组合应力

σ=σ_c+ψ_wγ_wσ_w=（11+1.0×1.4×3.85）N/mm²=16.4N/mm²。

【例5.2.2】 正方形筒中筒结构底层柱的轴力计算

条件：世界贸易中心为110层方形塔楼，高412m，平面尺寸为63.5m×63.5m，采用筒中筒结构，外筒为密柱框筒，底层每边有19根箱形截面钢柱，柱距3.05m。箱形柱截面为686mm×813mm，壁厚平均为90mm，柱截面面积A₀=0.263m²，角柱适当加强（图5.2.1）。

世界贸易中心总体高宽比h/d=412/63.5=6.491。大楼位于大西洋海边，平均风荷载为2200N/m²，房屋结构底层总弯矩M为

图 5.2.1

假定：（1）把世界贸易中心塔楼看做嵌固在地面的悬臂梁。

（2）筒中筒结构在水平荷载作用下，内筒的作用比外框筒作用相对较小，近似估算时先只考虑外框筒的作用。

（3）外框筒结构密柱间有刚性横梁相连，近似看做是共同工作的整体箱形截面，暂不考虑轴向变形的影响。

（4）角柱只有4根，近似与中间柱一样对待；风荷载取平均值。

要求：箱形柱承担的轴心力。

答案：（1）若忽略平行于x—x轴的两侧外墙的抵抗力，假定仅由迎风面和背风面承担所有由风载产生的弯矩（图5.2.2）。

在室外地面处，外墙背风面中每一个箱形柱承担的轴心力。

迎风面和背风面各有n=19根柱，横截面A_c=0.2630m²，截面惯性矩为

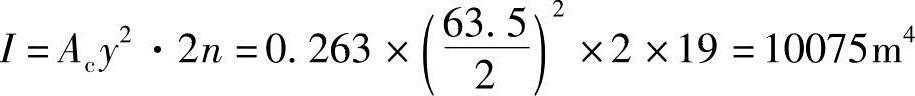
边柱承担的最大应力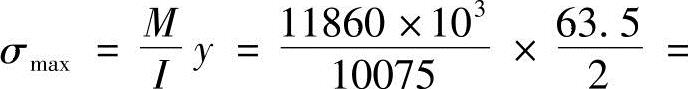，每根柱承担的轴心力N_w=A_cσ_max=0.263×37380=9830kN。

（2）由迎风面、背风面的外墙和平行于x—x轴的两侧外墙共同承担所有由风载产生的弯矩（图5.2.3）。

图 5.2.2

(www.xing528.com)

图 5.2.3

在室外地面处，外墙背风面中每一个箱形柱承担轴心力。

为简化计算，沿风荷载方向的框筒柱近似按“拍扁”后的等效“腹板”计算，则“腹板”的等效厚度。

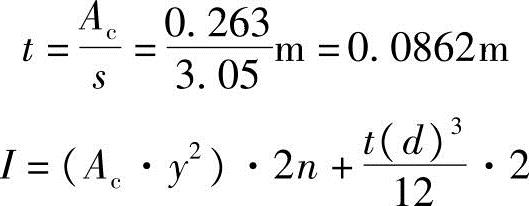
式中 A_c——柱截面面积；

s——柱间距；

n——每边的柱数；

y——框筒柱离截面中心的距离；

d——结构总宽度。

则房屋结构的总体截面惯性矩

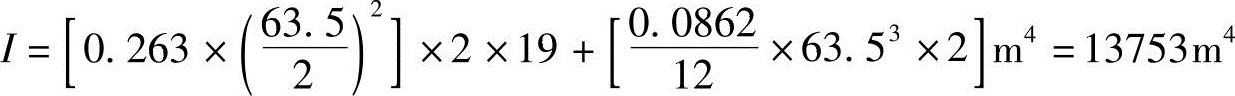
边柱由风载引起的最大附加应力为

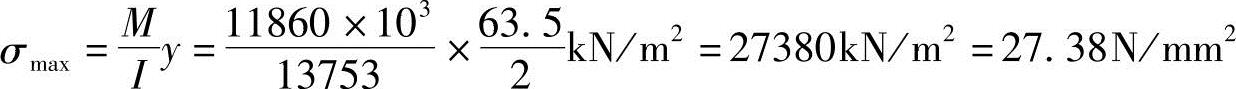
即风载引起的柱内最大附加应力为

σ_w=27.38N/mm²

单柱由风荷引起的附加内力为

N_w=A_cσ_max=0.263×27380kN=7200kN

【例5.2.3】 矩形筒体结构底层柱的轴力计算

条件：某矩形框筒，平面尺寸见图5.2.4a，总高度H=93m，承受均布水平力q=20kN/m。简化成双槽形截面处理，等效槽形截面见图5.2.4b。角柱为L形，其截面面积A₃=5.76m²、形心坐标y=0.90m。中柱截面面积A₁=A₂=A₄=A₅=0.96m²，槽形截面惯性（略去各柱自身惯性矩）I=3056.5m⁴。

结构底层总弯矩M=20×93²/2=86490kN·m。

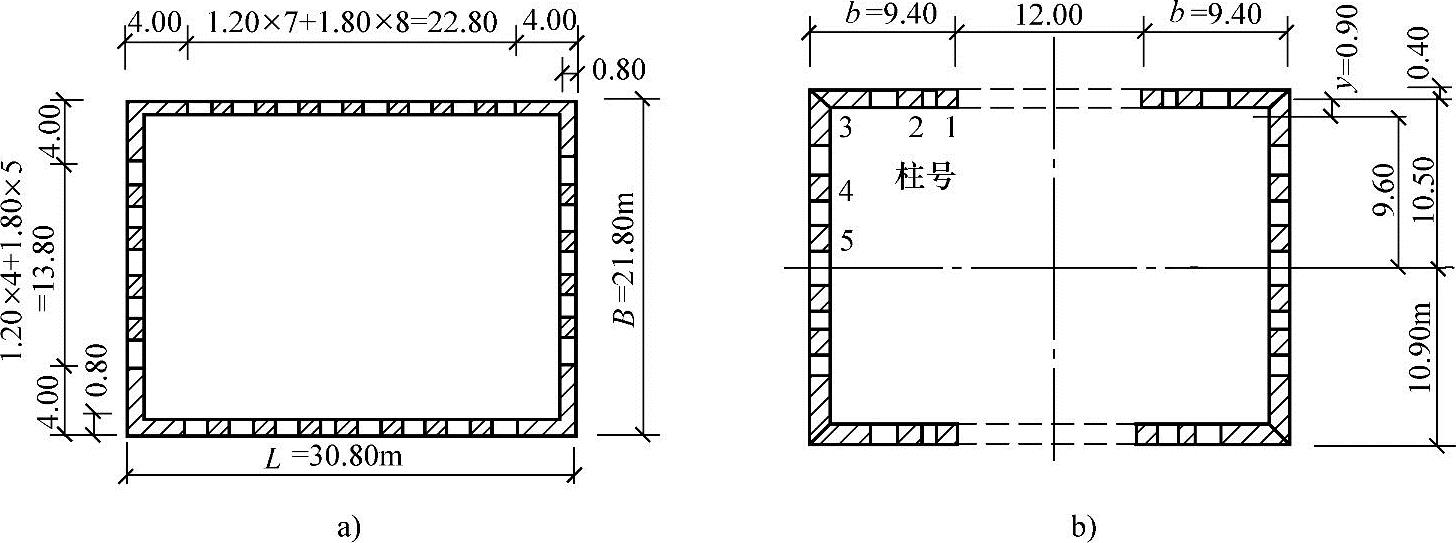
图 5.2.4

a）结构平面 b）等效平面

要求：确定底层1号柱、2号柱、3号柱的轴力。

答案：

（1）底层1号柱和2号柱的轴力N₁=N2底层1号柱和2号柱承担的应力值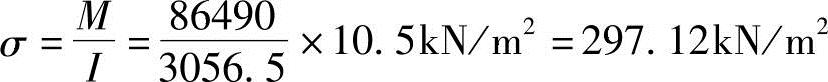承担的轴力N₁=N₂=297.12×0.96=285.2kN

（2）底层3号柱的轴力N3底层3号柱承担的应力值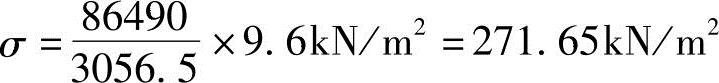承担的轴力

N₃=271.65×5.76kN=1564.7kN