1.试题回顾
【试题3.3.1】 整体小开口剪力墙的正应力分布(1999年)
在水平荷载作用下的某高层剪力墙结构,其中四种剪力墙的截面正应力分布如图3.3.1所示,试根据应力图形判断,其中哪一种属于整体小开口剪力墙?
【试题3.3.2】 双肢剪力墙按整体小开口剪力墙考虑的连梁折算惯性矩(2000年)
某16层建筑的一片双肢剪力墙,其墙肢宽度和沿竖向刚度均相等,其各层连梁的折算惯性矩I=5.12×10-3m4,根据计算,其整体性判别指标α=8、I0/I=0.89。试问,在只变更各层连梁折算惯性矩I0值,而不改变墙肢截面尺寸和连梁计算跨度的情况下,连梁折算惯性矩I0(m4)的最小值应取以下何项数值时,上述双肢剪力墙可按整体小开口墙考虑?
(A)Ib=6×10-3 (B)Ib=7×10-3
(C)Ib=8×10-3 (D)Ib=9×10-3
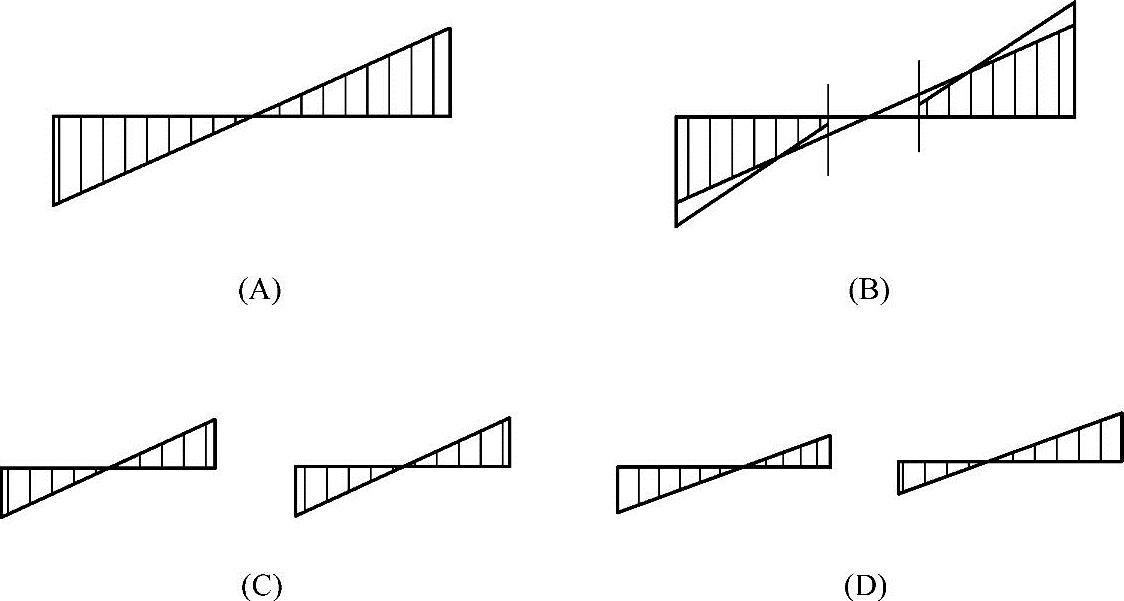
图 3.3.1
【试题3.3.3】 双肢剪力墙的连梁平均支座弯矩设计值(2001年)
某建造于大城市市区的28层公寓,采用钢筋混凝土剪力墙结构体系。平面为矩形,其中间的剪力墙的计算简图如图3.3.2所示。在如图所示的风荷载(标准值)作用下,试采用近似分析方法(将两个墙肢视为一拉一压,且其合力作用在墙肢的中心线上),估算每根连梁的平均支座弯矩设计值M(kN·m),最接近下列何项数值?
(A)±114 (B)±126 (C)±160 (D)±176

图3.3.2 横向剪力墙的计算简图
2.单榀双肢墙在水平荷载作用下的受力特点
双肢墙有两个墙肢和上下洞口间的各层连梁组成,墙肢的受力情况如下。
如图3.3.3所示的双肢墙,在水平力作用下,与悬臂梁相似,很容易求出剪力墙的弯矩图。
设离地面距离为x的某一水平截面处的弯矩为M,则由平衡条件知(图3.3.4a)

图 3.3.3

图3.3.4 剪力墙的受力特点
M=(M1+M2)+Na
式中 M1、M2——墙肢1、2单独承担的弯矩,称为墙肢的局部弯矩;
Na——由两个墙肢整体工作的组合截面所承担的弯矩,称为墙肢的整体弯矩;其中N为墙肢中的轴向力,一肢受压,一肢受拉;
a——两墙肢形心线间的间距,a=(a1+a2)。
现在再在连梁的跨中截开,并设该处连梁弯矩为零,见图3.3.4b。由平衡条件知
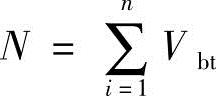
式中 Vbt——x截面以上第i层连梁的跨中竖向剪力。
n——x截面以上连梁的数目。
因此就有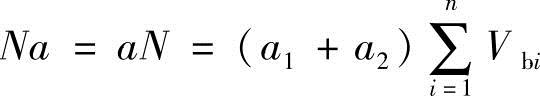 (https://www.xing528.com)
(https://www.xing528.com)
式中 Vbi(a1+a2)——x截面以上第i层连梁对两个墙肢产生的总约束弯矩; ——x截面以上所有连梁对墙肢约束弯矩的总和。
——x截面以上所有连梁对墙肢约束弯矩的总和。
可见:
1)任意截面x的弯矩M是由局部弯矩(M1+M2)和整体弯矩Na两部分组成的。整体弯矩大,局部弯矩就小。
2)任意一个截面x上的整体弯矩等于该截面以上所有连梁约束弯矩的总和,因此可以说,整体弯矩是由连梁提供的。
3)任意一个截面x上墙肢的轴向力等于该截面以上所有连梁竖向剪力的总和。
同时,也可理解为墙肢截面上的正应力是由两部分组成的:
1)第一部分是按各个单独的墙肢截面计算的由墙肢局部弯矩M1和M2产生的;第一部分正应力在各墙肢截面上的总和为零,即不产生墙肢轴向力。
2)第二部分是按组合截面由整体弯矩Na产生的。第二部分各墙肢截面上正应力的总和就等于该墙肢的轴向力N。
整体弯矩越大,说明两个墙肢共同工作的程度越大,越接近于整体墙。所以整体弯矩的大小反映了墙肢之间协同工作的程度,这种程度称为剪力墙的整体性。因为整体弯矩是由连梁对墙肢的约束提供的,而连梁的刚度又与洞口的大小有关,所以剪力墙的受力特点与洞口的大小和形状有关。
以图3.3.5所示带一列洞口的剪力墙为例,当洞口较小时,如图3.3.5c所示,洞口对结构内力分布的影响可忽略不计,整个剪力墙受力仍相当于一竖向悬臂构件。在侧向力作用下,剪力墙水平截面内的正应力分布在整个截面高度范围内呈线性分布或接近于线性分布,仅在洞口附近局部区域有应力集中现象发生,但从整体来看,洞口对墙体内力的影响可以忽略不计。这类剪力墙即为整截面剪力墙。
如果剪力墙上开洞很大,如图3.3.5a所示,连梁的刚度很小,其结果是由于连梁过分削弱,所以说它的整体性最差,剪力墙水平截面内的正应力分布在二个墙肢截面高度范围内呈线性分布或接近于线性分布。墙肢轴力所产生的整体弯矩很小,已能忽略不计。外荷载产生的弯矩由两个墙肢内的局部弯矩平衡。
当剪力墙开洞大小介于上述两者之间时,剪力墙在侧向荷载作用下的受力特性也介于上述两种情况之间。这一范围内的剪力墙分为整体小开口剪力墙与双肢剪力墙(当墙体上开有多列洞口时称为多肢墙或连肢墙)两种,如图3.3.5b所示。这时整个剪力墙水平截面上的正应力不再呈一直线分布,由于连梁传递弯矩的作用,墙肢内的由下到上的弯矩分布不再像悬壁杆一样呈一光滑的抛物线,而是呈齿状分布。
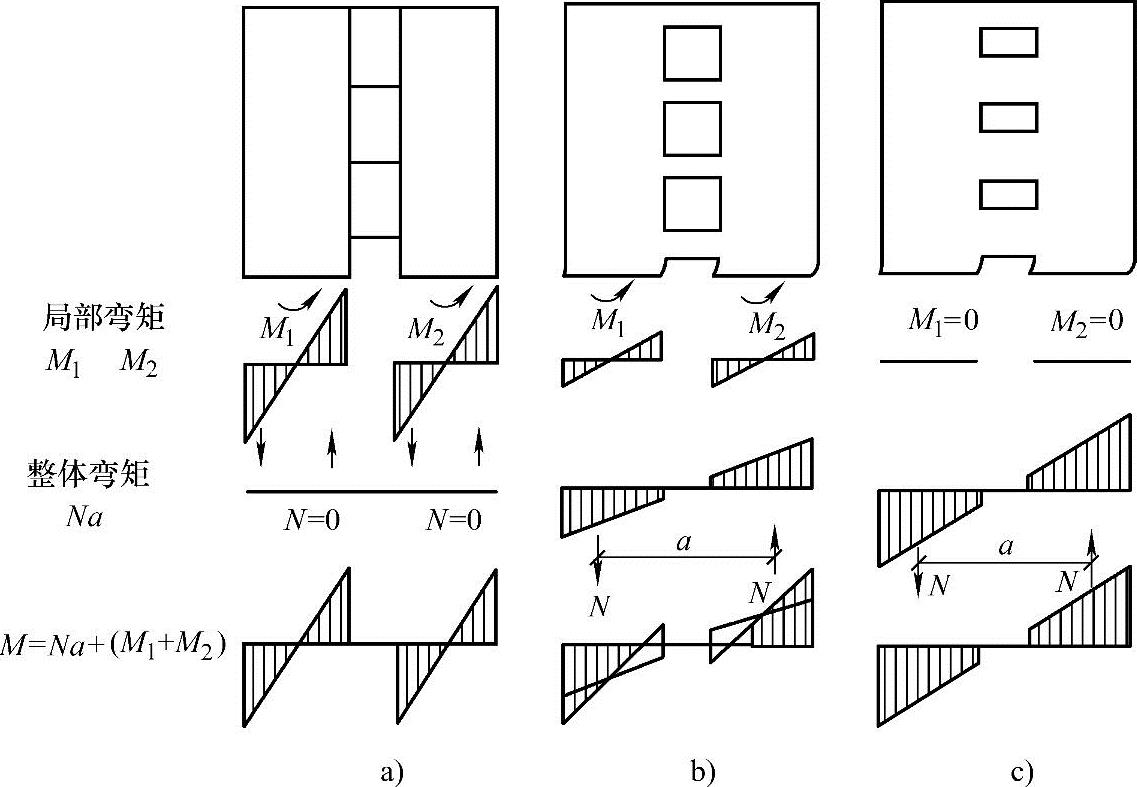
图 3.3.5
【例3.3.1】 双肢剪力墙连梁支座弯矩估算
条件:某建造于大城市市区的28层公寓,采用钢筋混凝土剪力墙结构体系。平面为矩形,共6个开间,横向剪力墙间距为8.1m,其中间的剪力墙的计算简图如图3.3.6所示。在如图3.3.7所示的风荷载(标准值)作用下。
要求:确定每根连梁分担的平均剪力值。
答案:剪力墙底部截面承受风荷载产生的弯矩M(设计值):
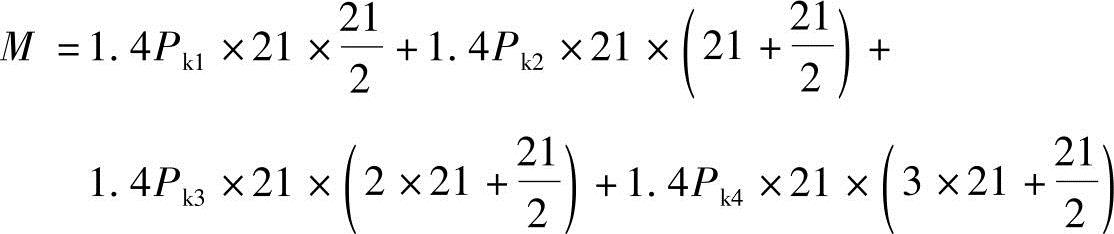
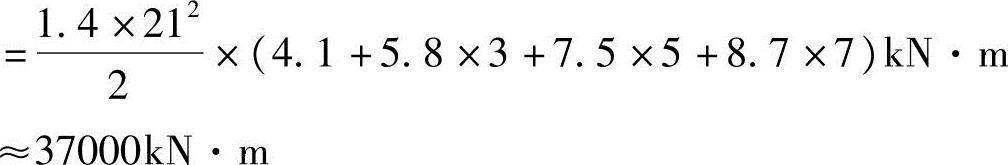

图3.3.6 横向剪力墙的计算简图
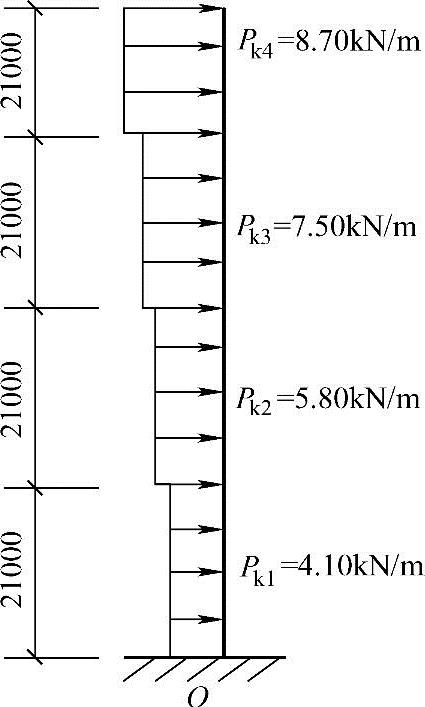
图3.3.7 受力简图
墙肢承受的轴力为 ,此处L=(2.5+7.8)m=10.3m
,此处L=(2.5+7.8)m=10.3m
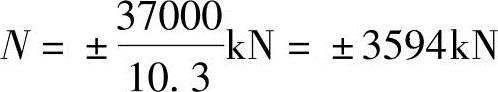
每根连梁平均分担的剪力值:
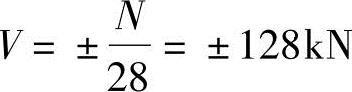
每根连梁平均承受的弯矩值
M=±V×1.25=±160kN·m(反弯点在连梁中间)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




