过盈量的大小是由工作时受力情况决定的。由于过盈配合常用在传动轴系中,所以下面我们着重分析传递扭矩时过盈量的计算。
1)传递扭矩的计算
根据主机的最坏功率和转速,主机发出的最大扭矩为
![]()
式中,Mmax——主机最大扭矩(N·m);
Nmax——主机最大功率(kW);
nmax——主机最大功率时轴的转速(r/min)。
常取安全系数为2.7,则传递扭矩为
M=2.7Mmax
2)配合面间比压p的计算
当配合面间的比压p只用来传递扭矩时,其比压
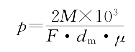
式中,F——接触面积(mm2);
dm——被包容件的直径(圆锥时为平均直径)(mm);
μ——摩擦系数。
3)过盈量Δ与配合面间比压p的关系
根据材料力学厚壁圆筒计算公式,有
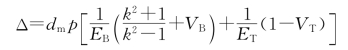
式中,EB——包容件材料弹性模数,铜质取11.7×104(MPa);
ET——被包容件材料的弹性模数,铜质取20.6×104(MPa);
VB——包容件材料泊松比,铜质取0.34;
VT——被包容件材料泊松比,铜质取0.26;
k——包容件内、外平均直径的比值(k=Dm/dm);
Δ——过盈量(mm)。
将上式变换得
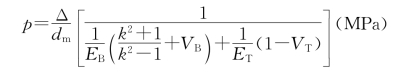
在工作时,由于离心力作用而使套合表面的比压减小,其减小值一般为5%~11%。一方面由于这部分计算工作繁杂,另一方面在选取安全系数时已经考虑了离心力的影响,所以一般可不必再次进行计算。
4)不同材料过盈配合时温度对过盈量的影响
由于工作和组装时温度不同,使得配合件因热膨胀系数不同而产生过盈量的变化。例如,根据规范规定,铜质包容件与钢质被包容件配合时,其工作最高温度为35℃,如安装温度为t且低于35℃,则由于温度升高,将使过盈量减少而应增加的过盈量计算如下:
(1)圆柱配合
Δr=d(λB-λT)(35-t)(mm)
式中,λB——包容件的线膨胀系数,铜质为18×10-6(1/℃);
λT——被包容件的线膨胀系数,钢质为11×10-6(1/℃)。
(2)圆锥配合
圆锥配合时,设锥度为S(按规范规定S≤1/15)。当温度增加时,其径向过盈量的增加与圆柱配合相同,只要将d换为平均直径dm即可计算出来。另外,由于两配合件的轴向位移会使得过盈量增大,所以应减少装配时的过盈量,其计算公式如下:
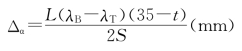
式中,L——包容件长度(mm)。
综合考虑,应增加的径向过盈量为
ΔT=Δr-Δα
总过盈量
ΔH=Δ+(Δr-Δα)
包容件和被包容件的尺寸在测量时,若温度不同,则应计入温度差别而引起的过盈量的变化,其值为
Δt=d[λB(t2-tg)-λT(t1-tg)](mm)
式中,t1——被包容件测量尺寸时的工作温度(℃);(https://www.xing528.com)
t2——包容件测量尺寸时的工作温度(℃);
tg——安装时的温度(℃);
Δt——应减小的过盈量。
5)被包容件相对于包容件的轴向位移量及位移图
当锥度配合时,轴向位移量
l=(ΔH+4G)/S
式中,G——因粗糙度而增加的过盈量,通常为0.0025~0.01mm。
由于位移量和温度成线性关系,为了工作方便,常根据0℃和35℃时的轴向位移量在坐标系上绘出温度-轴向位移线。如图1.50所示,根据装配时的温度可以求出某一温度安装时l的值。为了放大l的比例,可选取原点处不为零,以提高作图的精度。

图1.50 温度-轴向位移线
6)零位问题
当螺旋桨安装时,为了获得准确的轴向压入量,确定螺旋桨的零线位置是很重要的。在零线位置时桨与轴正好完全接触,配合既没有间隙也没有过盈。确定零线位置的方法较多,实际中用得较多的是实测法。
首先对螺旋桨施加一轴向推力F0,该力不包括桨重力的轴向分力和桨与轴间的摩擦力。此时将千分表转到零位读数,然后将轴向力加大到F1,读出千分表读数l1,再依次将轴向力加大到F2,F3,…,Fi,同时读出千分表读数l2,l3,…,li(一般读出4~5点即可),以F为纵坐标、l为横坐标作F-l图。
因为在弹性变形范围内,所以各点的连线为一直线。设连线的延长线与l轴交于A点,则点A即为螺旋桨轴向压入量的零位。用液压法装桨时,一直压到轴向压入量为l即可(如图1.51(a)所示)。用扩孔式液压装桨时,初始阶段同液压法,即先压入2~3mm的轴向压入量,待求出零位线后暂停轴向压入,向桨、轴配合面泵油,使配合孔扩大,而后继续把螺旋桨压到需要的轴向压入量,且该轴向压入量应以零位线开始计算(如图1.51(b)所示)。
用实测法求得的零位线显然是合理的,A点表示当轴向压入负荷为零时轴向压入量也为零,这时螺旋桨毂孔和螺旋桨轴刚刚接触,零位就该从这种情况开始算起。
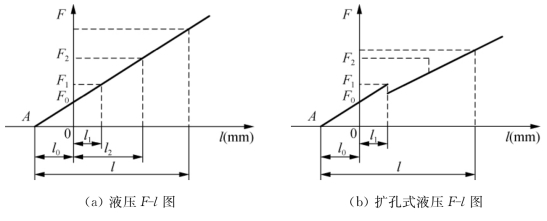
图1.51 螺旋桨压入量零位的确定
7)强度校核
过盈配合时,其强度校核常从配合零件的应力状态分析开始,多以包容件为分析对象。
(1)应力状态
设内半径为r,平均内径为dm,外半径为R,平均外径为Dm,内表面压力为p,则内表面处切向应力σrt为
![]()
径向应力σrr为
σrr=-p(MPa)
外表面处切向应力σRt为
![]()
径向应力σRR=0。
(2)外表面的应力允许值
强度校核时外表面的切向应力应当不超过40MPa,否则将产生应力腐蚀。即
![]()
得
p≤20(k2-1)(MPa)
(3)内表面的应力允许值
强度校核时内表面的综合应力σE≤0.6σS,其中σS为包容件即螺旋桨材料的屈服极限(N/mm2)。其应力排列次序如下:
![]()
σ2=σx=0
σ3=σrr=-p
根据第四强度理论,有
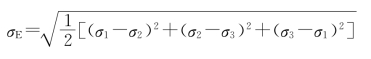
即
![]()
得
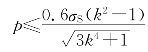
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




