珠江三角洲网河低水位变化及关键问题处理

5.2.5.1　卵石夹沙河床水流的有效挟沙能力

根据韩其为等［29］的研究，卵石夹沙河床水流中的悬移质与床沙的交换是单向的，水流仅从床沙中冲起细颗粒泥沙而悬沙中粗颗粒泥沙几乎不落淤。此时挟沙能力由两部分组成，一部分是悬移质来沙全部计入挟沙能力，另一部分是床沙中可冲颗粒部分地掀起后计入挟沙能力，即

式中　S*（ω）——全部悬移质挟沙能力。

式中　S*（ω11）——床沙中能够悬浮部分的挟沙能力；

　　　P1——床沙中可悬颗粒所占百分数；

　　　PmL——床沙级配；

式中　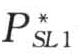——相应的挟沙能力级配。

5.2.5.2　沙质河床水流的有效挟沙能力

沙质河床水流中的悬移质中粗颗粒与床沙中细颗粒在不断发生交换，悬移质中粗颗粒部分落淤，而床沙中细颗粒被掀起。根据韩其为的研究，此时挟沙能力由三部分组成：第一部分是悬移质中细颗粒部分，它从累计效果看，不参与床沙交换，即常说的冲泻质部分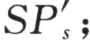；第二部分是悬移质中粗颗粒部分落淤到床面后与床沙发生交换后再部分地掀起后计入挟沙能力SP"s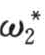S*（）/S*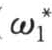（）；第三部分是从床沙中可冲颗粒中部分地掀起后计入挟沙能力

式中　k——冲泻质与床沙质的分界粒径；

　　　S*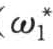（）——全部床沙挟沙能力；

　　　S*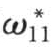（）——床沙中能够悬浮部分挟沙能力。

以上是SL≤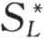含沙量小于挟沙能力情况，而当SL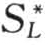＞时

5.2.5.3　非均匀沙起动概率及非均匀沙推移质输沙率

1.非均匀沙起动概率

非均匀床沙交换过程中，大小粒径在床面的暴露程度不一样，使得大小颗粒之间的相互影响十分复杂。颗粒处在床面上位置不同，则颗粒所受水流作用力也不同。暴露于平均床面以上的粗颗粒，所受水流作用力相对要大一些；位于平均床面以下的细颗粒，处于大颗粒的尾流区，受到大颗粒的荫蔽作用。我们采用参数ξ来反映颗粒的暴露和荫蔽作用，并用床沙几何平均粒径Dm作为床沙的代表粒径，经Little-Mayer、Gessler、Ashida-Michiue、刘兴年、陆永军等试验资料及San Lus河资料回归得到荫暴系数表达式（Lu Yongjun等，1992）［30］

粒径为DL组泥沙的临界Shields数为

将式（5.39）、式（5.40）代入Gessler的泥沙停留在床面不动概率公式得到第L组泥沙的起动概率为(www.xing528.com)

2.非均匀沙推移质输沙率

采用作者从水流功率理论出发导出的非均匀沙推移质输沙率公式（陆永军等，1992）［31］

式中　τ0——水流拖曳力，τ0=γRJ；

PmL——床沙级配；

　　　qL——第L组泥沙停留在床面的概率，可由修正后的Gessler公式（5.41）算得；

　　　θcrL—临界Shields系数，由式（5.40）计算。

当床沙为均匀沙时，式（5.42）转变成

式（5.44）与Samage等、Gilbert实验资料、长江新厂（二）站沙质推移质输沙资料的比较表明，计算值与实测值吻合较好（陆永军等，1992）［31］。

5.2.5.4　挟沙能力公式系数KO及指数m

挟沙能力系数KO及指数m根据含沙量饱和河段含沙量S与［Q3 B/A4 w］m之间的关系确定。长江中游冲淤验证计算表明，KO=0.014～0.017，指数m采用韩其为［11］得到的值，m=0.92。

5.2.5.5　恢复饱和系数α的选取

若各种粒径组恢复饱系数α取不同值，验证计算工作量很大，数值试验表明，不饱和输沙公式中恢复饱和系数α可以不随粒径变化，一般情况下，悬移质中各粒径组泥沙均发生冲淤时，α=0.25；悬移质中粗颗粒落淤而床沙中细颗粒被冲刷时，α=0.5；悬移质中粗颗粒不落淤，床沙中可冲颗粒部分均发生冲刷时，α=1.0。

5.2.5.6　混合层厚度Em

Em与床沙特性有关，计算表明，对于卵石夹沙河床，冲刷初期Em=1.0～2.0m，冲刷后期，Em=0.5～1.0m；对于沙质河床，Em相当于沙波波高，一般取为2.0～3.0m。

5.2.5.7　推移质与悬移质的划分

推移质与悬移质的划分采用通常悬移指标ω/ku*的概念，ω/ku*≥5时为推移质，当ω/ku*＜5时为悬移质。