地面沉降对高铁竖曲线的影响

在线路纵断面的变坡点处设置的竖向圆弧称为竖曲线。常用的竖曲线线形有抛物线形和圆弧形两种，目前主要采用圆弧形竖曲线。竖曲线分为凸形和凹形两种。凸形的竖曲线的视距条件较差，需选择适当的半径以保证行车安全，向上的竖向离心力，使车辆有上浮倾向，在横向力作用下，容易产生脱轨事故。凹形的竖曲线，视距一般能得到保证，但会产生离心力，因此应选择适当的半径来控制离心力不要过大，以保证行车的平顺和舒适。

目前规定，在允许的最大沉降的条件下，调整轨面高程后的竖曲线半径应能满足下式要求：

式中　Rsh——轨面圆顺的竖曲线半径（m）；

　　　Vsj——设计最高速度（km/h）。

因竖曲线为圆弧曲线，为便于计算，各种倾斜的坐标系总可以通过坐标旋转利用图中的坐标系来表达，a 为半弦长，b 为弧高，如图5.3-1所示。

图5.3-1　竖曲线示意图

联立以上两个解可得R 与a、b 的表达式：R=。因此，竖曲线半径R 随a 呈平方增大，随b 呈反比变化。对于凹形的竖曲线也可以得到同样的表达式。

利用以上推导，计算在不利的情况下，即由于竖曲线中部产生相对于两端部较小的沉降，导致b 值增大，使竖曲线半径减小。下面为分别计算在a、b（a、b 的几何意义见图5.3-1）变化条件下，对R 的影响。图5.3-2 为a 对应b 增大5%、10%、20%、30%、40%、50%、100%、200%和300%对竖曲线R 产生的影响；图5.3-3 为b 对应a 减小5%、10%、20%、30%、40%和50%对R 的影响。

图5.3-2　不同弧高时竖曲线与半弦长关系

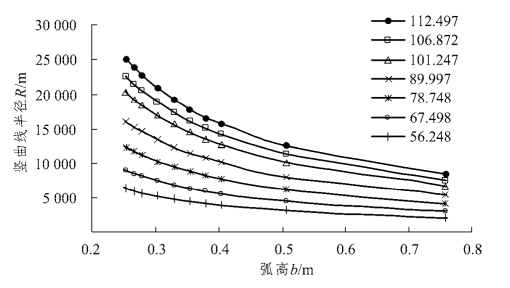
图5.3-3　不同半弦长时竖曲线与弧高关系

对于凸曲线而言，R 值推算与实际符合。a 为A、D 之间的距离，为半弦长，b 为C、D 之间的距离，为弧高。Sf 为A 点的实际沉降，Svc 为Sf 在垂直于AB 方向的分解量，Shc 为沿AB 方向的分解量（如图5.3-4所示）。(www.xing528.com)

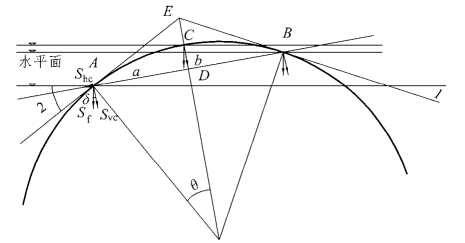
图5.3-4　凸竖曲线示意图

由几何关系可以得到

则变化后的a′值和b′值分别为

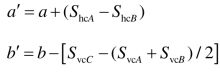
其中，SvcA，SvcB，SvcC 和 ShcA，ShcB，ShcC后面的A、B、C 为分别对应于A、B、C 处的沉降分量，可以由δ 角度和原位沉降Sf 换算得到。

然后把a′值和b′值代入公式R　=　，即可计算变化后的R 值。

对于凹曲线也可以由同样的方法计算得到变化后的a、b、R 值。

若在竖曲线长度范围内，地面沉降对于竖曲线来讲是均匀的，不至影响竖曲线的线形，且不产生差异沉降，则对线路的影响是微小的。

若在竖曲线长度范围内，表现出来的沉降是不均匀的，会在线路上形成新的变坡点，车辆通过时，振动和局部加速度的增大会使乘车舒适度降低并会进一步恶化线路的运营条件。

由于在变坡点处车辆的通过易产生大的振动和加速度，对线路造成冲击，会对竖曲线产生影响。

对于凹形的竖曲线，地面沉降可能会产生以下4 种不同的影响：第一，在竖曲线的变坡处如果发生相对于两端大的沉降，会使竖曲线半径减小，圆心移动，竖曲线长度减小；第二，竖曲线端部产生相对于变坡处较大的变形，这时可能使竖曲线的半径增大，长度增大，圆心移动；第三，端部局部发生大的变形，可能会在端部形成两个半径较小的竖曲线，中部由直线或者大半径的曲线相连；第四，一端产生相对另一端较大的变形，会形成大半径的竖曲线，竖曲线长度可能会减小，圆心位置发生移动。

对于凸形的竖曲线，地面沉降会有以下3 种不同的影响：第一，竖曲线整体的逐渐的不均匀沉降会使竖曲线圆心、半径、长度都发生变化；第二，竖曲线中部产生较大变形，会在端部形成两个半径较小的竖曲线，中部由直线或者大半径的曲线相连，也有可能形成一条大半径竖曲线；第三，端部产生大变形，竖曲线半径减小，圆心移动，曲线长度变短。