影响半径系指地下水开采时从井轴至降落漏斗边缘静止水位的距离,是比较重要的水文地质参数。下面以完全潜水井为例,说明影响半径的确定方法。
根据裘布依公式的假设,假定含水层是水平的、均质各向同性的;水流呈轴对称的径向流动;在距井轴一定距离R 上,水位下降为零;水流运动符合达西定律。那么假定完全潜水井井底位置在水平不透水层上,其含水层厚度为H,未抽水前地下水的天然水面为水平面A—A。当从井中抽水,井中和四周附近地下水位降低,在含水层中形成了以井中垂直轴线对称的浸润漏斗面,如图2.3-1所示。

图2.3-1 完全潜水井示意图
在离井中心r 处渗流浸润面上的点的高度为z,z′为该点到天然水面的距离,而过水断面为一与井同心的圆柱面,其面积为w=2πrz,又设其渗流为渐变渗流,则过水断面上各点的水力坡度皆为J=dz/dr。
根据达西定律,过水断面上的各点渗流流速u 都相等,因而断面平均流速v 也等于渗流流速u,故v=u=kJ,k 为土体渗透系数。
经此渐变圆柱面的渗流量为

进而得到潜水井的浸润曲线方程为

式中 r0——井的半径;
h——井中水位。
对于井的影响半径R,在浸润漏斗上,有半径r=R 的一个圆,在R范围内,浸润漏斗的下降H-z 趋于零,即天然地下水位不受影响,距离R 即称为井的影响半径,则出水量Q 为

结合上述关系,最终获得浸润线的计算关系,即z′和r 的关系:

以下分析主要参数对浸润线的影响,采用的基本参数如表2.3-1所示。
表2.3-1 浸润线分析的主要参数

1.抽水井半径的影响
当土体渗透系数为 1×10-4cm/s,对于不同水位降深和井半径条件下的浸润曲线如图2.3-2~图2.3-6 所示,其中井半径r0 分别为0.2 m、1 m、2 m、3 m 和4 m。从图中可知,井半径对浸润曲线的变化速率有一定影响,对影响半径无影响。对于相同的水位降深,浸润曲线起点和终点的高度是一致的,井半径r0 则改变了浸润曲线各点的r 值,r0 增大,相应r增大,随着r0 的增大,浸润曲线趋于缓和。

图2.3-2 浸润曲线(r0=0.2 m)

图2.3-3 浸润曲线(r0=1.0 m)(https://www.xing528.com)

图2.3-4 浸润曲线(r0=2.0 m)
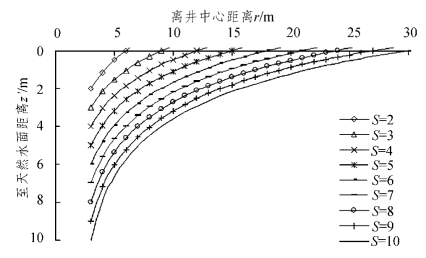
图2.3-5 浸润曲线(r0=3.0 m)

图2.3-6 浸润曲线(r0=4.0 m)
2.渗透系数的影响
根据表2.3-2 典型土体渗透系数的一般取值范围,当井半径r0 为1 m时,对于不同水位降深和土体渗透系数条件下的浸润曲线如图2.3-7~图2.3-11 所示,渗透系数分别为1.0×10-3、5.0×10-4、1.0×10-4、5.0×10-5 和1.0×10-5cm/s。从图中可知,渗透系数对浸润曲线的影响较大,k 越大,浸润曲线越缓和。对于相同的水位降深,随着渗透系数k 的增大,影响半径R 逐渐增大。
表2.3-2 典型土体渗透系数的范围


图2.3-7 浸润曲线(k=1.0×10-3cm/s)

图2.3-8 浸润曲线(k=5.0×10-4cm/s)

图2.3-9 浸润曲线(k=1.0×10-4cm/s)

图2.3-10 浸润曲线(k=5.0×10-5cm/s)

图2.3-11 浸润曲线(k=1.0×10-5cm/s)
3.水位降深的影响
水位降深对影响半径具有较大影响。对于土体不同渗透系数,影响半径随水位降深的变化如图2.3-12 所示,影响半径随水位降深呈线性变化,对于同一水位降深 S,渗透系数越大,影响半径越大。渗透系数 k从1.0×10-5cm/s 变化到5.0×10-3cm/s。当S=5 m 时,影响半径从4.7 m 增大至106.1 m;当S=9 m 时,影响半径从8.5 m 增大至190.9 m。

图2.3-12 影响半径随水位降深的变化
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




