二个正态总体的假设检验-《概率论与数理统计》

设总体X～N（μ1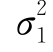，），Y～N（μ2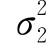，），X1，X2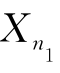，…，和Y1，Y2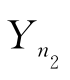，…，分别是来自总体X和Y的样本且相互独立.它们的样本均值和样本方差分别为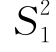，和，.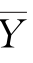

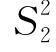1.已知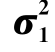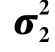，，检验假设H0：μ1=μ2

检验假设H0：μ1＝μ2等价于检验H0：μ1－μ2＝0，由于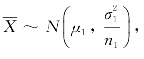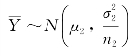及X1，X2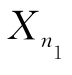，…，与Y1，Y2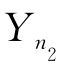，…，的独立性，可知

因此，当H0成立时，统计量

由

得拒绝域为

例4　一药厂从某药材中提取某种有效成分，为了提高得率，改进提炼方法.现对同一质量的药材，用新、旧两种方法各做了10次试验，其得率分别为

旧方法 76.2，76.0，77.3，72.4，74.3，78.4，76.7，75.5，78.1，77.4.

新方法 77.3，80.0，79.1，77.3，80.2，81.0，79.1，82.1，79.1，79.1.

设两个样本相互独立，都来自正态总体，X～N（μ1，3），Y～N（μ2，3）.试问：新旧两种方法相比，得率有否提高（α＝0.1）？

解　依题意，检验假设H0：μ1＝μ2，备择假设H1：μ1＜μ2.我们选择统计量

作为检验统计量.当H0为真时，U～N（0，1），由样本值求得79.43，于是统计量

由α＝0.1，查标准正态分布表得因为|u|＝4.13＞1.645，落在拒绝域内，即应拒绝假设H0.又因为统计量u＝－4.13＜－u0.01＝－2.33，故接受备择假设H1：μ1＜μ2，即表明新提炼方法的得率比旧方法有显著提高.

2.已知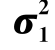==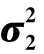σ2，但其值未知，检验假设H0：μ1=μ2

引用下述统计量T作为检验统计量：

式中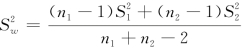，.当H0为真时，T～t（n1＋n2－2），由

得拒绝域为

例5　某种物品在处理前后分别取样分析其含脂率，得到数据如下：

处理前 0.29，0.18，0.31，0.30，0.36，0.32，0.28，0.12，0.30，0.27.　　　

处理后 0.15，0.13，0.09，0.07，0.24，0.19，0.04，0.08，0.20，0.12，0.24，

假定处理前后含脂率都服从正态分布且方差不变，问处理后含脂率的均值比处理前是否显著减少（α＝0.05）？(www.xing528.com)

解　设处理前后含脂率的均值分别为μ1和μ2.依题意，需要检验假设

H0：μ1＝μ2，备择假设H1：μ1＞μ2.

分别求出处理前后样本均值和样本方差如下：

由α＝0.05，查表得t0.05（19）＝1.7291.由于

所以拒绝H0，即认为处理后含脂率的均值比处理前显著减少.

本题所做的是所谓单边检验，即当H0为真时，T～t（n1＋n2－2），由

P(T≥tα(n1＋n2－2))＝α

得拒绝域为

这类检验在前面提到的各种检验中也普遍存在，可类似地进行讨论.

3.两个正态总体方差的假设检验

设X1，X2，…，Xn1与Y1，Y2，…，Yn2分别为来自总体N（μ1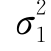，）和N（μ2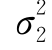，）的样本，且相互独立.现在需要检验假设H0：＝.

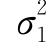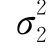我们只讨论μ1、μ2未知的情况.因为样本方差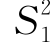、是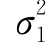、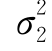的无偏估计量，在H0成立时，它们不应相差太多，即比值

应接近于1，否则当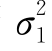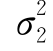＞时，F有偏大的趋势；在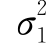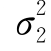＜时，F有偏小的趋势.由于F～F（n1－1，n2－1）.所以可取F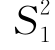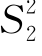＝/作为检验统计量.

例6　试对例5中的数据检验假设（α＝0.05）

解　n1＝10，n2＝11，α＝0.05，

拒绝域为

或

现在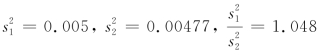，即有

故接受H0，即认为两总体方差相等.这也表明例5中假设两总体方差相等是合理的.