概率论与数理统计中的区间估计方法

上面我们讨论了参数的点估计，如果用样本观察值x1，x2，…，xn代入估计量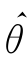（X1，X2，…，Xn）中，就得到一个数值（x1，x2，…，xn）作为真值θ的近似值，结果简单明确；但作为一个近似值，它与真值间总有偏差，在点估计中没有反映出近似值的精确度，又不知它的偏差范围，也就是说，它不能表示出估计值的精确程度和可靠程度.在实际问题中往往需要由样本估计出未知参数的一个范围，并且能指出有多大把握预言未知参数不超过这个范围.这个范围通常以区间形式给出，就是用区间作为未知参数的估计，并且说明这个区间包含参数真值的概率.这样的区间称为置信区间，这种估计称为参数的区间估计.

定义3　设总体X的分布中含有未知参数θ，对于给定值α，0＜α＜1，若由样本X1，X2，…，Xn确定的两个统计量θ1（X1，X2，…，Xn）和θ2（X1，X2，…，Xn）满足

则称区间（θ1，θ2）是参数θ的置信度为1－α的置信区间.其中θ1，θ2分别称为置信下限和置信上限.1－α称为置信度.

置信区间不同于一般的区间，它是随机区间.对于样本的每个观察值相应确定一个区间.式（6.1）的意义是，反复抽样多次（各次的样本容量都为n），得到众多的区间，在这些区间中有的包含参数θ的真值，有的不包含θ的真值，当置信度为1－α时，包含θ真值的约占100（1－α）%，不包含θ真值的仅占100α%；但要注意的是，这里不说θ的真值以100（1－α）%的概率落入该区间，这是因为θ真值客观上是确定值，不是随机变量.

由于正态随机变量的广泛存在，讨论正态总体中参数的区间估计有重要的意义.

1.单个正态总体N（μ，σ2）数学期望μ的区间估计

（1）已知总体方差D（X）＝σ2，求μ的置信区间.我们知道样本均值是总体均值μ＝E（X）的一个点估计.由第五章定理1知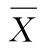～，所以随机变量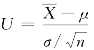服从标准正态分布，即

在随机变量U中只含待估参数μ，而不含其他未知参数，并且它服从与任何未知参数无关的已知分布.对于给定的置信度1－α，在标准正态分布表中查得，使得

亦即

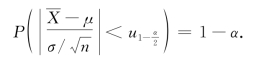
由于不等式

等价于不等式

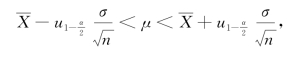
从而有

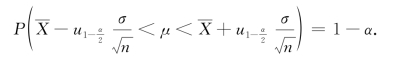
因此，我们得到μ的一个置信度为1－α的置信区间

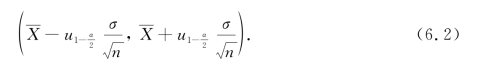
这里要说明的是是使服从标准正态分布的随机变量U满足的值.由于

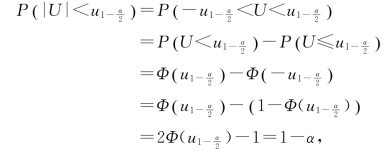
所以

查附表2可得也称为正态分布的双侧α分位点.

例8　已知某炼铁厂的铁水含碳量在正常情况下服从正态分布N（μ，0.1082）.现测量5炉铁水，其含碳量分别是

4.28，4.40，4.42，4.35，4.37 (%)

试求总体均值μ的置信区间（α＝0.05）.

解　由样本值算得样本均值

又由α＝0.05得，查正态分布表得代入式（6.2）计算

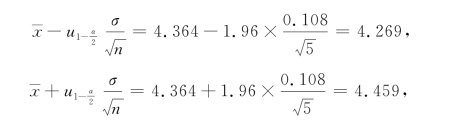
即得μ的置信度为0.95的置信区间是（4.269，4.459）.

（2）未知方差，求μ的置信区间.因为样本方差S 2是总体方差σ2的无偏估计，所以σ2未知时，可用S 2来估计σ2.又

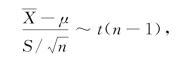
由t分布的双侧α分位点，有

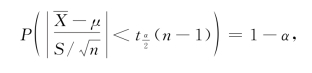
于是得μ的置信度为1－α的置信区间为

例9　设某种油漆的9个样品，其干燥时间（以小时计）分别为

6.0，5.7，5.8，6.5，7.0，6.3，5.6，6.1，5.0.

设干燥时间服从正态分布N（μ，σ2）.求μ的置信度为0.95的置信区间.

解　由样本值算得＝6，s＝0.5745.由，查表可得t0.025（8）＝2.306.于是可得

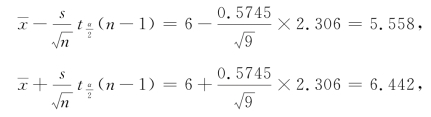
故μ的置信度为0.95的置信区间是（5.558，6.442）.

2.单个正态总体方差σ2的区间估计

在μ未知的情形下，样本方差S 2是σ2的无偏估计量，考虑随机变量χ2＝是由样本确定的只含待估参数σ2的函数，并且由第五章定理1知它服从自由度为n－1的χ2分布，即

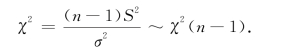
对于给定的置信度1－α，利用χ2分布表，可确定两数λ1和λ2，使得

P(λ1＜χ2＜λ2)＝1－α.

因为χ2分布的密度函数图形不对称，所以不能得到对称的置信区间，这时习惯上由(https://www.xing528.com)

来确定λ1和λ2.查χ2分布表得满足

图6.1

即

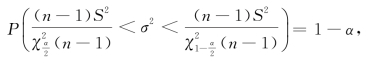
如图6.1所示，从而得到σ2的置信度为1－α的置信区间

例10　常用投资的回收利润率来衡量投资的风险.随机地调查了26项年回收利润率（%）得样本标准差S＝15（%）.设回收利润率服从正态分布，试求方差σ2的置信度为0.95的置信区间.

解　n＝26，S＝15，（25）＝40.646，（25）＝13.120，故

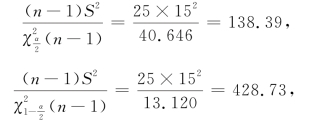
所以σ2的置信度为0.95的置信区间为（138.39，428.73）.

3.两个正态总体均值差的区间估计

设总体X～N（μ1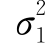，），Y～N（μ2，）.X1，X2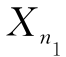，…，是X的一个样本，Y1，Y2，…，Yn2是Y的一个样本，而和分别是X，Y的样本均值和样本方差.

（1）当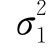，均为已知时，求均值差μ1－μ2的置信区间.因为X，Y是μ1和μ2的无偏估计，所以是μ1－μ2的无偏估计，且知

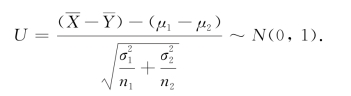
在给定置信度1－α时，应有

从而得到μ1－μ2的置信度为1－α的置信区间为

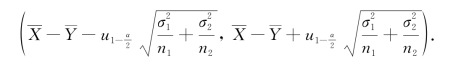
（2）当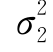＝＝σ2，但σ2未知时，求均值差μ1－μ2的置信区间.由于随机变量

在随机变量T中只含待估参数μ1－μ2，与单个正态总体σ2未知求μ的置信区间类似，对于给定的置信度1－α，立即可得μ1－μ2的置信区间为

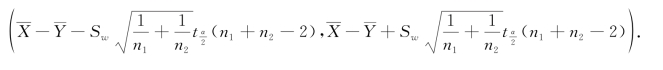
（3）当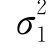，均未知，此时只要n1，n2都很大（实际应用上一般大于50即可），则可用

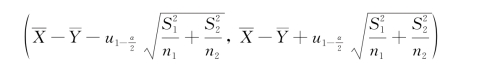
作为μ1－μ2的置信度为1－α的近似的置信区间.

例11　为了比较甲、乙两种灯泡的使用寿命，随机地从甲种灯泡中抽取6只，测得＝1021小时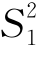，＝262；随机地从乙种灯泡中抽得8只，测得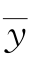＝985小时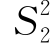，＝302.假定两种灯泡寿命都服从正态分布，且方差相等.试求甲、乙两种灯泡平均寿命之差的置信度为0.95的置信区间.

解　因为

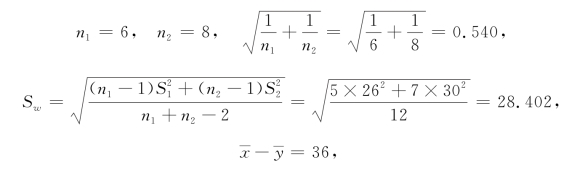
所以甲、乙两种灯泡平均寿命之差的置信度为0.95的置信区间是

(36－t0.025(12)×28.402×0.540，36＋t0.025(12)×28.402×0.540)，

即（2.56，69.44）.

4.两个正态总体方差比的区间估计

设总体X～N（μ1，），总体Y～N（μ2，），X1，X2，…，是来自总体X的样本，Y1，Y2，…，是来自总体Y的样本，且两个样本相互独立.我们仅讨论总体均值μ1，μ2为未知的情况.

由于样本方差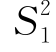和分别是总体方差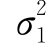和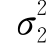的无偏估计，由于

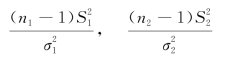
分别服从自由度为n1－1和n2－1的χ2分布，注意到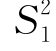和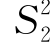相互独立，由F分布定义知

对于给定的置信度1－α，容易得到的置信区间为

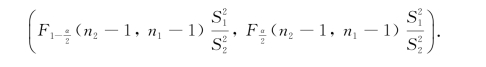
方差比的置信区间的含意是，若的置信上限小于1，则说明总体X的波动性较小；若的置信下限大于1，则说明总体X的波动性较大.若置信区间包含数1，则不能从这次试验中判定两个总体波动性的大小.

例12　设两位化验员各自独立地对某种聚合物含氯量用相同的方法各作10次测定，其测定值的样本方差依次为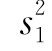＝0.5149，＝0.6065，设，分别为两位化验员所测定的总体的方差，总体均为正态的，求方差比的置信度为0.95的置信区间.

解　由于总体期望未知，故应选用随机变量

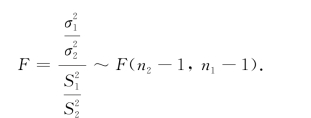
由于n1＝n2＝10，α＝0.05，故查F分布表得

将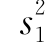＝0.5419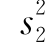，＝0.6065代入

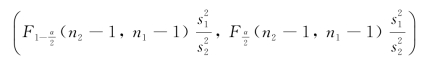
中，得置信度为0.95的置信区间为（0.221，3.59）.