概率论与数理统计-无偏性评价标准

上面所介绍的方法说明，对总体X的一个参数，我们可以用不同的方法求得它的估计量.那么，在同一参数的许多可能的估计量中，哪一个是最好的估计量呢？对此，我们有下面三个最一般的标准.

1.无偏性

如果x1，x2，…，xn是样本的一个观察值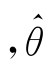（x1，x2，…，xn）作为θ的估计值，它与真值之间总有偏差，或大于真值，或小于真值，但希望多次估计值的理论平均值应等于真值θ.这一性质称之为无偏性.

定义　设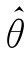（X1，X2，…，Xn）为未知参数θ的估计量，且满足

则称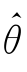是θ的无偏估计量.

例5　设X1，X2，…，Xn是总体X的一个样本，总体X的期望为E（X）＝μ，求证：（其中Ci≥0，且）是总体期望μ的无偏估计量.

证　由于X1，X2，…，Xn与X同分布，故有

E(Xi)＝E(X)＝μ， i＝1，2，…，n.

又由期望的性质

因而是μ的无偏估计量.　　　　　□

特别地，当时，即对样本均值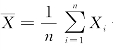也有，所以不论总体X服从什么分布，只要E（X）存在，就可用作为它的无偏估计.

由这个例子还可以看出，同一个参数可以有很多无偏估计量.

例6　设X1，X2，…，Xn是总体X的一个样本，总体X的期望E（X）＝μ，方差D（X）＝σ2，且μ，σ2均为未知，求证：样本方差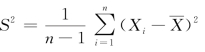是σ2的无偏估计量.

证　由于

从而有

又由

故(www.xing528.com)

于是

由此可见，样本方差是总体方差的无偏估计量，而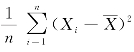就不是总体方差σ2的无偏估计.　　　　　□

2.有效性

大家知道，同一参数可能有许多无偏估计量，在这些估计量中哪一个更好呢？自然地认为应以对真值的平均偏差较小者为好.由于方差是刻画偏离程度的量，在样本容量相同的情况下，方差愈小表示估计值与真值的偏离愈小，估计量取值愈稳定，所以无偏估计以方差小者为好.由此得估计量的有效性.

定义1　设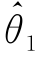（X1，X2，…，Xn）和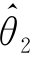（X1，X2，…，Xn）都是θ的无偏估计量，如果

则称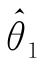比有效.

例7　求证：当样本容量n≥3时，用样本均值作为E（X）的无偏估计量，比用作估计量有效.

证　由例5知，题设中给出的E（X）的4个估计量均是无偏估计量.又因为

当n≥3时，有

所以比X1，有效.　　　　　□

3.一致性

估计量是样本的函数，估计值与参数的真值不一定相等，自然希望当样本容量n充分大时，估计值稳定于参数的真值，这就是估计量的一致性.

定义2　设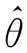（X1，X2，…，Xn）是参数θ的估计量，若当n→∞时 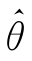依概率收敛于θ，即对任意ε＞0，有

则称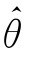 是θ的一致估计量.

可以证明，样本均值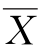是总体均值μ的一致估计量，样本方差S 2是总体方差σ2的一致估计量，样本k阶矩Ak是总体k阶矩的一致估计量.另外，由最大似然法得到的估计量，在一定条件下也具有一致性.