最大似然估计法及其应用

当总体分布类型已知时，对未知参数点估计的另一种理论上较优良、适用范围较广的是最大似然估计法.这种估计方法是利用总体的密度函数表达式和样本所提供的信息，建立未知参数θ的估计量.

最大似然估计法的理论依据是最大似然原理.大家知道，概率大的事件比概率小的事件易于发生.例如，在一只口袋内有黑白两种颜色的球共100只，只知道它们数目之比为99∶1.今从袋内摸出一球，结果为白球.我们自然更多地相信袋内白球为99只，黑球为1只.这就是“最大似然”的想法.现在我们根据样本情况估计参数时也应用这一想法.如果一次随机试验的结果得到样本观察值x1，x2，…，xn，它是已经发生的随机事件，可以设想样本取到这个值的事件是以最大概率使其发生，因而就取使这一概率达到最大的参数值作为未知参数的估计值.

下面根据这个想法来估计总体的未知参数.设总体X的密度函数（或分布律）为f（x，θ），其中θ为未知函数.x1，x2，…，xn是样本X1，X2，…，Xn的一个观察值.因为样本X1，X2，…，Xn的联合分布密度为，所以对给定的样本值x1，x2，…，xn，是θ的函数，记为L（θ），即

L(θ)＝ f(xi，θ)＝f(x1，θ)f(x2，θ)…f(xn，θ).

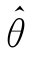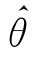我们把L（θ）称为样本的似然函数.它反映了样本X1，X2，…，Xn取观察值x1，x2，…，xn的概率大小.又因为θ取值的不同直接影响L（θ）大小的变化，而我们又认为样本取这一观察值的概率最大，所以选取使似然函数L（θ）达到最大的参数值 作为θ的估计值，这就是最大似然估计法.而把使L（θ）达到最大值的 称为参数θ的最大似然估计值.显然， 与样本值x1，x2，…，xn有关，记做（x1，x2，…，xn），而相应的统计量 （X1，X2，…，Xn）称为参数θ的最大似然估计量.

对于求总体参数θ的最大似然估计值（或估计量）的方法可由高等数学求函数极值的方法得到.当似然函数L（θ）在参数θ取值区间上只有一个驻点时，这个驻点就是L（θ）的最大值点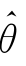， 即为参数θ的最大似然估计值.因为L（θ）往往以乘积形式出现，而L（θ）和ln L（θ）在同一θ处取得最值，所以求参数θ的最大似然估计值可用求ln L（θ）的最大值点来实现.这样做往往更为简便.

例3　设总体X服从指数分布，其密度函数为

式中，未知参数θ＞0.X1，X2，…，Xn是来自总体X的一个样本.求参数θ的最大似然估计量.

解　似然函数为

式中，x1，x2，…，xn是相应于样本X1，X2，…，Xn的一个样本值.取对数得

令＝0，得(www.xing528.com)

解得θ的最大似然估计值为

所以θ的最大似然估计量为

例4　设总体服从正态分布N（μ，σ2），其中μ和σ2为未知参数.X1，X2，…，Xn是来自X的一个样本.求μ，σ2的最大似然估计量.

解　X的密度函数为

似然函数为

取对数得

令

联立得

从而μ和σ2的最大似然估计量分别为