在实际问题中，经常遇到需要用样本来估计有关总体的某些未知参数.例如，为了确定一批灯泡的质量，就要知道这批灯泡的使用寿命.根据经验知道，它的使用寿命服从正态分布N（μ，σ2），但并不知道μ和σ2的具体数值.为了判断这批灯泡的质量，只能通过样本估计出它的平均寿命及寿命长短的差异程度，也就是利用样本估计正态分布的两个未知参数μ和σ2.这就是参数估计问题.这个问题的一般提法是，设总体X的分布中包含未知参数θ（可以是一个，也可以是几个）.由样本X1，X2，…，Xn构造适当的统计量
（X1，X2，…，Xn）去估计未知参数θ（需估计几个未知参数，就构造几个统计量）.统计量
（X1，X2，…，Xn）也称为参数θ的估计量.
进行参数估计的总体，不一定知其分布类型.当总体分布类型已知时，可估计其中的未知参数.而当总体分布类型未知时，可估计总体的数字特征.参数估计有许多方法，主要是点估计和区间估计.
对参数θ的估计量
（X1，X2，…，Xn），用样本的一个观察值（x1，x2，…，xn）代入，算出具体数值θ ^ （x1，x2，…，xn）来估计未知参数θ，称
（x1，x2，…，xn）为θ的估计值.显然，估计量是样本的函数，是一个随机变量.对样本的不同观察值，θ的估计值往往是不同的.在不至引起混淆的情况下，统称估计量和估计值为估计，并都简记为
.这种关于参数θ的估计叫做参数θ的点估计.根据构造估计量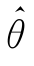
方法的不同，点估计又分为矩估计法和最大似然估计法.(www.xing528.com)
从总体X中取得样本观测值后，由参数的点估计方法，我们可以求得未知参数θ的估计值.但是，点估计对估计的精度与可靠性没有作出明确的回答，而在实际问题中，人们不仅需要求出未知参数的估计值，而且往往还需要了解这些估计值的精度与可靠性.区间估计在一定程度上弥补了点估计的不足.用样本对未知参数θ可能取值的范围作出估计，并指出这个范围包含参数θ真值的概率.这样的范围通常由样本X1，X2，…，Xn构造的两个估计量
（X1，X2，…，Xn）和
（X1，X2，…，Xn）为端点所组成的区间
表示.这种关于参数θ的估计称为区间估计.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
