【摘要】：设X～N（0，1），Y～χ2（n），且X，Y相互独立，则称随机变量所服从的分布是自由度为n的t（Student）分布，记为T～t（n）.t（n）分布的概率密度为其图形如图5.4所示.图5.4图5.5t（n）分布的概率密度是偶函数，其图形形状类似标准正态概率密度的图形.可以证明，当n→∞时，t（n）分布的极限分布就是标准正态分布.对于给定的正数α，0＜α＜1，满足的数tα（n）称为t（n）分布的上α
设X～N（0，1），Y～χ2（n），且X，Y相互独立，则称随机变量
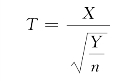
所服从的分布是自由度为n的t（Student）分布，记为T～t（n）.
t（n）分布的概率密度为
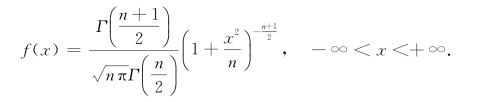
其图形如图5.4所示.
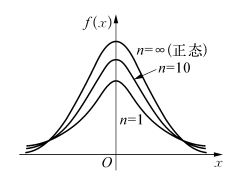
图5.4
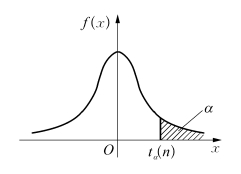
图5.5
t（n）分布的概率密度是偶函数，其图形形状类似标准正态概率密度的图形.可以证明，当n→∞时，t（n）分布的极限分布就是标准正态分布.
对于给定的正数α，0＜α＜1，满足
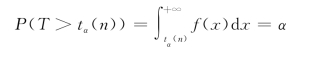
的数tα（n）称为t（n）分布的上α分位点，如图5.5所示.查t分布表可得相应的分位点.例如查表得t0.01（12）＝2.6810.(www.xing528.com)
在今后的学习过程中，还会用到t（n）分布的双侧α分位点.对于给定的正数α（0＜α＜1）.满足
P(|T|＜t*)＝1－α
的数t*称为t（n）分布的双侧α分位点.由于t（n）分布的密度函数是偶函数，所以P（T≤－t*）＝P（T≥t*）.于是
P(|T|＜t*)＝P(－t*＜T＜t*)
＝P(T＜t*)－P(T≤－t*)
＝(1－P(T≥t*))－P(T≥t*)
＝1－2P(T≥t*)
＝1－α，
因此
也即
可以看到t（n）分布的双侧α分位点t*就是其上
分位点
（n）.而
（n）可以查t 分布表求得.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
