在这里,我们介绍两种关于总体分布的近似求法:经验分布函数与直方图.
1.经验分布函数
若总体为X,求分布函数F(x).
设x1,x2,…,xn为总体的一组样本观察值,将它们按由小到大的顺序排列,得到
![]()
定义4 令

则称Fn(x)为经验分布函数.
当样本X1,X2,…,Xn取定一组观察值后,Fn(x)就确定了.它可视为一个概率分布为
P(X=xk)=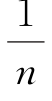 ,k=1,2,…,n,
,k=1,2,…,n,
的离散型随机变量X的分布函数.
Fn(x)的图形是跳跃式上升的一条阶梯形曲线.若观察值不重复,则每一跃度为![]() ;若有重复(相同)时,跃度为
;若有重复(相同)时,跃度为![]() 的倍数.
的倍数.
其次,经验分布函数Fn(x)的值依赖于样本观察值.所以是样本的函数.又因为它不含未知参数,所以Fn(x)是一个统计量.格里汶科(W.Glivenko)在1933年证明了以下的结果:对于任一实数x,当n→∞时,Fn(x)以概率1一致收敛于分布函数F(x),即
![]()
因此,对于任一实数x,当n充分大时,经验分布函数的任一个观察值Fn(x)与总体分布函数F(x)只有微小的差别,从而在实际上可作F(x)来使用.
例1 随机地观察总体X,得10个数据如下:
3.2,2.5,-4,2.5,0,3,2,2.5,4,2.
将它们由小到大排列为
-4,0,2,2,2.5,2.5,2.5,3,3.2,4.
其经验分布函数是

2.直方图
当总体X为连续型随机变量时,总体分布可以用总体密度函数f(x)来表示,而f(x)需要我们用样本来推断.下面介绍的频率直方图是求f(x)的最简单而有效的近似求法.
设x1,x2,…,xn为X的样本X1,X2,…,Xn的一组观察值.我们采用以下步骤作出直方图:
(1)将总体X的一组样本值x1,x2,…,xn按大小次序排列,得
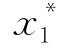 ≤
≤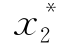 ≤…≤
≤…≤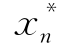 .(https://www.xing528.com)
.(https://www.xing528.com)
(2)选取a(略小于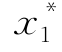 )和b(略大于
)和b(略大于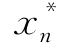 ),则所有的样本值都落入区间(a,b]中.在(a,b]内插入k-1个分点,
),则所有的样本值都落入区间(a,b]中.在(a,b]内插入k-1个分点,
a=t0<t1<t2<…<tk-1<tk=b,
将(a,b]分成k个小区间:
(t0,t1],(t1,t2],…,(tk-1,tk].
Δti=ti-ti-1是第i个小区间的长度,称为第i组组距.各组组距可以相等,也可以不等,但每个小区间都要包含若干个样本值.小区间的个数k一般可取8至15个,太少或太多均不易显示分布特征.另外分点的值ti应比数据的有效数字多一位.
(3)用唱票的办法,数出样本值落在区间(ti-1,ti]中的频数ni,并计算出频率
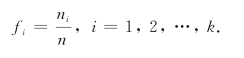
(4)在x轴上标出各分点,以(ti-1,ti]为底边,画出高度为fi/Δti的矩形,便得到直方图.其中第i个小矩形的面积ΔSi是样本落入区间(ti-1,ti]的频率,是概率的近似值,即
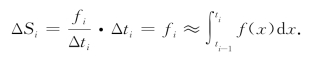
连接直方图矩形上边缘的曲线便是f(x)的近似图形.
如果在步骤(4)中用组中间值![]() 的频率分布代替样本观察值的频率分布,我们便可求出经验分布函数Fn(x).
的频率分布代替样本观察值的频率分布,我们便可求出经验分布函数Fn(x).
例2 某洗涤剂厂为了保证质量,对某天生产的洗涤剂进行抽查,测得100瓶洗涤剂重量的数据如下:
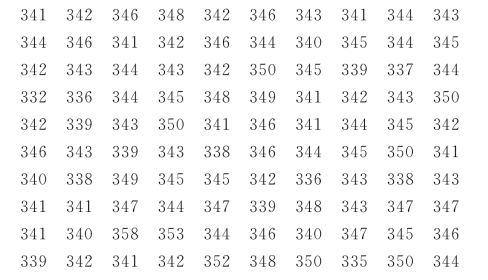
试画出直方图及近似f(x)曲线,并求出经验分布函数F100(x).
解 因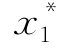 =332,
=332,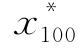 =358,故可取(a,b]为(331.5,358.5],把(a,b]分成长度为3的9个小区间(组),列出频数与频率表如下:
=358,故可取(a,b]为(331.5,358.5],把(a,b]分成长度为3的9个小区间(组),列出频数与频率表如下:
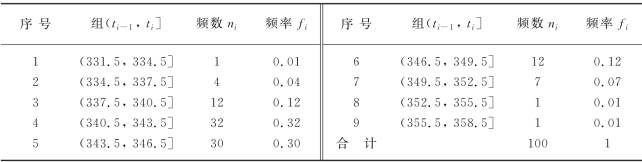
根据表上数据作出直方图,如图5.1所示.
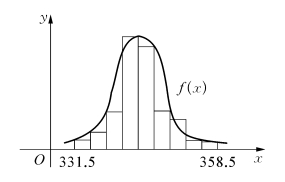
图5.1
从直方图可以看出,X应服从正态分布N(μ,σ2),μ≈343.8,σ≈4.05.
再用组中间值的频率分布

可求出经验分布函数F100(x).
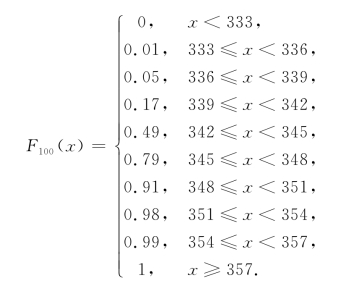
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




