概率论与数理统计-协方差与相关系数

对于二维随机变量（X，Y），我们给出一个描述X，Y间关系的一个数字特征.

定义1　设（X，Y）是一个二维随机变量，若E（（X－E（X））（Y－E（Y）））存在，则称它是X和Y的协方差，记为cov（X，Y），即

cov(X，Y)＝E((X－E(X))(Y－E(Y)))

称

为X和Y的相关系数.它是一个无量纲的量.

当ρXY＝0时，称X和Y是不相关的或无关的.

根据期望、方差的性质可得下面计算公式：

例1　已知二维随机变量（X，Y）的分布律为

其中，p＋q＝1，求相关系数ρXY.

解　由上面的分布律，可以得到边缘分布律

X，Y均服从（0-1）分布，故知

E(X)＝p， D(X)＝pq，

E(Y)＝p， D(Y)＝pq.

再由式（3.16）得

cov(X，Y)＝E(XY)－E(X)E(Y)

＝0×0×q＋0×1×0＋1×0×0＋1×1×p－p×p

＝p－p 2＝p(1－p)＝pq.

ρXY＝

例2　设二维随机变量（X，Y）的密度函数为

求cov（X，Y）.

解　E（X）＝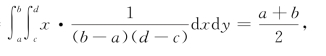

协方差的性质：

(1)cov(X，Y)＝cov(Y，X)；

（2）cov（a X，bY）＝ab cov（X，Y），a、b为常数；

(3)cov(X＋Y，Z)＝cov(X，Z)＋cov(Y，Z).

以上性质可根据协方差的定义直接推得.

在概率论里，有时需要将随机变量“标准化”，即对任意的随机变量X，若其期望E（X）、方差D（X）均存在，且D（X）＞0，则称

为X的标准化随机变量.通过简单计算可得E（X*）＝0，D（X*）＝1.这也正是标准化随机变量所具有的特征.

若将随机变量X，Y标准化，

由相关系数定义可知

相关系数的性质：

(1)|ρXY|≤1.

证　由

D(X*±Y*)＝D(X*)＋D(Y*)±2cov(X*，Y*)(www.xing528.com)

＝1＋1±2cov(X*，Y*)

＝2(1±ρXY)，

及D（X*±Y*）≥0得1±ρXY≥0.所以，|ρXY|≤1.　　　　　□

（2）|ρXY|＝1的充分必要条件是X和Y依概率1线性相关，即P（Y＝a X＋b）＝1，其中b，a≠0为常数.

证　由方差性质（4），知

P(Y＝a X＋b)＝P(Y－b－a X＝0)＝1

成立的充分必要条件是

D(Y－b－a X)＝E((Y－b－a X)2)－(E(Y－b－a X))2

＝E((Y－b－a X)2)＝0，

即

0＝E((Y－b－a X)2)

＝E(((Y－E(Y))－a(X－E(X))＋(E(Y)－a E(X)－b))2)

＝E((Y－E(Y))2)＋a 2E((X－E(X))2)＋(E(Y)－a E(X)－b)2 －2a E((Y－E(Y))(X－E(X))) ＋2(E(Y)－a E(X)－b)E(Y－E(Y)) －2a(E(Y)－a E(X)－b)E(X－E(X))

＝D(Y)＋a 2D(X)＋(E(Y)－a E(X)－b)2－2a cov(X，Y)＋0－0

＝ ＋(E(Y)－a E(X)－b)2.

上式右端三项均是非负的.要使上式成立必须每项为零，故由第二项为零，可得

即

|ρXY|＝1.　　　　　□

从上述性质可以看出，相关系数实质上是表示两个随机变量X与Y之间线性相关程度的一个量.当|ρXY|较大时，X与Y的线性联系比较紧密；当|ρXY|较小时，X与Y的线性联系比较不紧密.

特别地，当|ρXY|＝1时，X与Y的线性联系最紧密，即以概率1存在线性关系；而当|ρXY|＝0时，即ρXY＝0时，X与Y的线性联系最不紧密，此时我们称X，Y不相关.

由式（3.15）可知，若X与Y相互独立，有cov（X，Y）＝0，从而ρXY＝0.即X和Y相互独立，则X和Y不相关.反之，若X，Y不相关（没有线性关系），则X，Y不一定是相互独立的.这说明“相互独立”与“不相关”是两个不同的概念.

例3　若X～N（0，1），且Y＝X 2，问X和Y是否无关？

解　由于X～N（0，1），密度函数为偶函数，故有E（X）＝E（X 3）＝0.

cov(X，Y)＝E(XY)－E(X)E(Y)＝E(XX 2)－E(X)E(X 2)

＝E(X 3)－E(X 2)E(X)＝0.

得

这说明X和Y是不相关的.虽然X和Y无线性关系，但是有函数关系，所以X和Y不是独立的.

例4　若（X，Y）～N（μ1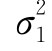，；μ2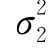，；ρ），求ρXY.

解　由于X～N（μ1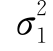，），Y～N（μ2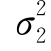，），所以，E（X）＝μ1，D（X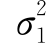）＝；E（Y）＝μ2，D（Y）＝.

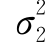令

则有

于是

可见二维正态随机变量（X，Y）的密度函数中的参数ρ就是X和Y的相关系数.