数学期望从一个角度描述了随机变量的特征.但是对一个随机变量来说，仅仅知道它的数学期望是不够的，我们还常常需要知道它的取值关于数学期望的偏离程度.例如，甲乙两个工人生产同一种零件，已知他们生产的零件的长度X1与X2的分布律为
容易算出E（X1）＝E（X2）＝30，这说明仅由零件长度的均值还无法判断两个工人的技术水平高低.此时，可以进一步考虑零件长度X与其均值E（X）的偏离程度|X－E（X）|的大小.而|X－E（X）|也是随机变量，因而可以用|X－E（X）|的均值即E（|X－E（X）|）来衡量X与E（X）的偏离程度.经计算可得
E(|X1－E(X1)|)＝0.70，
E(|X2－E(X2)|)＝0.86.
由此可以看出，甲生产的零件长度偏离其均值的程度较小，所以甲生产的零件长度比较均匀.从这个意义上说，甲的技术水平较乙为高.
然而，由于绝对值|X－E（X）|的数学期望E（|X－E（X）|）在计算上不方便，所以通常用E（（X－E（X））2）来描述随机变量与其数学期望的偏离程度.
定义1 设X是一个随机变量，若E（（X－E（X））2）存在，则称E（（X－E（X））2）为X的方差，记为D（X），即
D(X)＝E((X－E(X))2)
称与X具有相同量纲的量
为X的均方差或标准差.
方差实际上是随机变量X函数的期望，故由式（3.4）、（3.5）可知，若X为离散型随机变量，分布律为
P(X＝xk)＝pk， k＝1，2，…，
则有
若X为连续型随机变量，f（x）为密度函数，则有
除此之外，还有一个常用的计算方差的重要公式
证 D（X）＝E（（X－E（X））2）
＝E(X 2－2XE(X)＋(E(X))2)(www.xing528.com)
＝E(X 2)－2E(X)E(X)＋(E(X))2
＝E(X 2)－(E(X))2. □
例1 设随机变量X服从（0-1）分布，分布律为
P(X＝1)＝p， P(X＝0)＝1－p＝q.
求D（X）.
解 由式（3.2）知E（X）＝p.
E(X 2)＝12×p＋02×q＝p.
代入式（3.10）
D(X)＝p－p 2＝p(1－p)＝pq.
例2 设随机变量X的密度函数为
求D（X）.
解 E（X）＝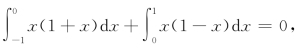
E(X 2)＝
于是
D(X)＝E(X 2)－(E(X))2＝
.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
