数学期望性质与线性组合，概率论与数理统计核心

在下面的讨论中，所遇到的数学期望均假设其存在，只对连续型随机变量给以证明，至于离散型随机变量的证明只要将积分换为类似的求和即可得到.

（1）设C为常数，则有E（C）＝C.

证　可将C看成离散型随机变量，分布律为P（X＝C）＝1，由定义知E（C）＝C.　　　　　□

（2）设C为常数，X为随机常量，则有

E(CX)＝CE(X).

证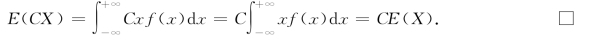　

（3）设X，Y为任意两个随机变量，则有

E(X＋Y)＝E(X)＋E(Y).

证　设二维随机变量（X，Y）的密度函数为f（x，y），边缘密度函数为fX（x）、fY（y），则由式（3.7）有

这个性质可以推广到任意有限多个随机变量的情形，即

E(X1＋X2＋…＋Xn)＝E(X1)＋E(X2)＋…＋E(Xn).

设a1，a2，…，an为常数，则有

E(a1 X1＋a2 X2＋…＋an Xn)＝a1E(X1)＋a2E(X2)＋…＋anE(Xn).

这表明随机变量线性组合的数学期望，等于随机变量数学期望的线性组合.

（4）设X和Y为相互独立的随机变量，则有

E(XY)＝E(X)E(Y).(www.xing528.com)

证　由于X和Y相互独立，（X，Y）的密度函数与边缘密度函数间有如下关系：

f(x，y)＝fX(x)fY(y).

由式（3.7）有

这一性质也可以推广到任意有限多个相互独立的随机变量之积的情况.若X1，X2，…，Xn相互独立，则有

E(X1 X2…Xn)＝E(X1)E(X2)…E(Xn).

例11　一送客汽车载有20位旅客，自出发地开出后，旅客有10个车站可以下车.如到达一个车站没有旅客下车就不停车.设每位旅客在各个车站下车是等可能的，以X表示停车的次数，求E（X）.

解　因为每位旅客每站下车的概率为，不下车的概率为.故可引入随机变量

则有X＝X1＋X2＋…＋X10.并且

由此可得

从而

E(X)＝E(X1＋…＋X10)

＝E(X1)＋E(X2)＋…＋E(X10)

＝10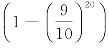＝8.787.

这表明汽车平均停车8.787次.

像本例这种将X分解为若干个随机变量之和，然后利用期望性质再求X期望的方法，具有一定的普遍意义，使用得当，可使复杂问题简单化.