【摘要】：，n，且它们相互独立，则和Z＝X1＋X2＋…＋Xn仍服从正态分布，且
设二维随机变量（X，Y）的函数为Z＝g（X，Y），Z是一维随机变量，故其分布函数为
FZ(z)＝P(Z≤z)＝P(g(X，Y)≤z)
若（X，Y）的密度函数为f（x，y），则Z的分布函数可表为
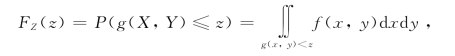
这样可以用f（x，y）在平面区域{g（x，y）≤z}上的二重积分表示.由此可得Z的密度函数为
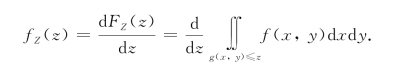
有了以上的结果，求随机变量函数的分布问题原则上算解决了，但具体计算仍有一定难度.
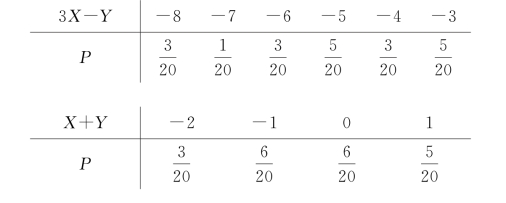
例7 设（X，Y）的分布律为
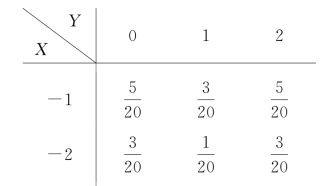
求：（1）Z＝3X－Y；（2）Z＝X＋Y的分布律.
解 列表如下
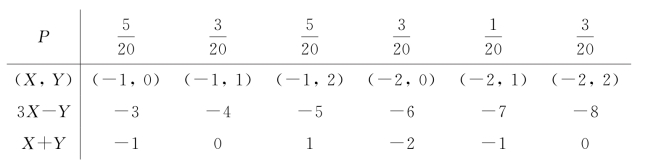
则
例8 设（X，Y）的密度函数为f（x，y），求Z＝X＋Y的密度函数.
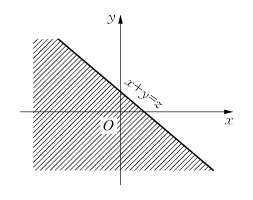
图2.18
解 如图2.18所示，
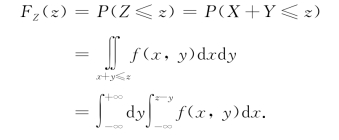
令x＝u－y，则(www.xing528.com)
所以
由于X，Y的对称性，又有
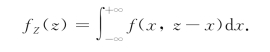
当X与Y相互独立时，有f（x，y）＝fX（x）fY（y），从而
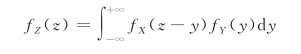
或
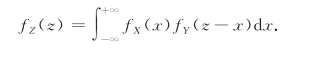
例9 设X与Y相互独立，且均服从标准正态分布，求Z＝X＋Y的密度函数.
解 由X与Y的相互独立性知，（X，Y）的密度函数为
f(x，y)＝fX(x)fY(y)，
而
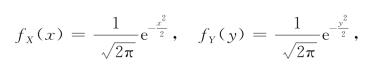
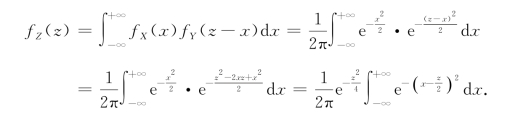
令
，则
即X＋Y～N（0，
）.
该例说明，两个相互独立的服从正态分布的随机变量的和仍服从正态分布.这个结论可以推广到有限多情形，即Xi～N（μi，
），i＝1，2，…，n，且它们相互独立，则和Z＝X1＋X2＋…＋Xn仍服从正态分布，且
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
