随机变量的独立性及其定义概率论与数理统计

例5的结论指出，一般情况下边缘分布不能确定联合分布，这里隐含着在特殊情况下，边缘分布还可以确定联合分布，这种特殊情况是由X与Y间的相互关系所决定的，我们把这种关系称为X与Y的相互独立性，下边给出具体定义.

定义3　若二维随机变量（X，Y）对任意实数x，y均有

成立，则称随机变量X与Y是相互独立的.式（2.10）也可写成如下形式：

F(x，y)＝FX(x)FY(y)，

式中，F（x，y）表示（X，Y）的联合分布函数；FX（x），FY（y）分别表示X，Y的分布函数.

若（X，Y）是离散型随机变量，则X与Y相互独立的充分必要条件是

P(X＝xi，Y＝yj)＝P(X＝xi)P(Y＝yj)，

即

pij＝pi·p·j， i，j＝1，2，…，

这里pij，pi·，p·j分别为（X，Y），X，Y的分布律.

若（X，Y）是连续型随机变量，则X与Y相互独立的充分必要条件是(www.xing528.com)

f(x，y)＝fX(x)·fY(y)，

式中，f（x，y），fX（x），fY（y）分别为（X，Y），X，Y的密度函数.

例6　若二维随机变量（X，Y）服从正态分布N（μ1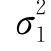，；μ2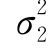，；ρ），试证X和Y相互独立的充分必要条件是ρ＝0.

证　（X，Y）的联合密度函数为

充分性　设ρ＝0，代入上式得

必要性　由X与Y的相互独立性，对任意实数x，y均有

f(x，y)＝fX(x)fY(y).

特别地，取x＝μ1，y＝μ2，代入上式有

即

因此有ρ＝0.　　　　　　　　□