二维连续型随机变量的密度函数

设二维随机变量（X，Y）的联合分布函数为F（x，y），若存在非负函数f（x，y），对任意实数x，y有

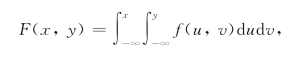
则称（X，Y）为连续型的二维随机变量，且称f（x，y）为二维随机变量（X，Y）的联合密度函数或概率密度.

联合密度函数具有如下性质：

(1)f(x，y)≥0；

(2)

凡满足（1）、（2）的任一个二元函数f（x，y），必定是某个二维随机变量的联合密度函数.

（3）若f（x，y）在点（x，y）处连续，则

（4）若G是平面上的一个区域，则有

根据联合分布函数与边缘分布函数的关系可求出边缘密度函数

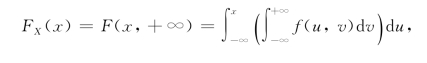
且有

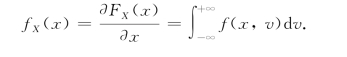
同理，

fX（x），fY（y）分别称为（X，Y）关于X，Y的边缘密度函数.

例2　已知（X，Y）的密度函数为

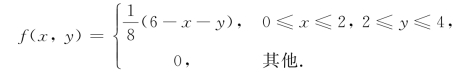
设：（1）D1为平面上由x≤1，y≤3所确定的区域，如图2.17（a）所示；（2）D2为平面上由x＋y≤3所确定的区域，如图2.17（b）所示.试求P（（x，y）∈Di），i＝1，2.

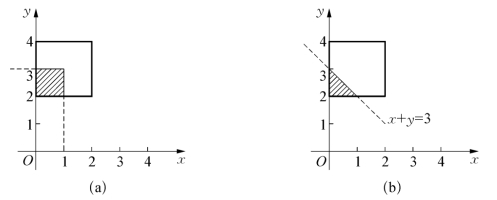
图2.17

解　（1）P（（x，y）∈D1）＝F（1，3）＝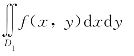

＝

＝

＝

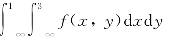
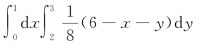
(2)P((x，y)∈D2)＝

＝

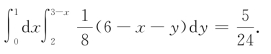
例3　已知二维随机变量（X，Y）的密度函数为

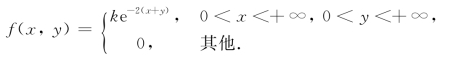
试求：（1）常数k；（2）联合分布函数F（x，y）；（3）边缘分布函数FX（x），FY（y）及边缘密度函数fX（x），fY（y）.

解　（1）由于

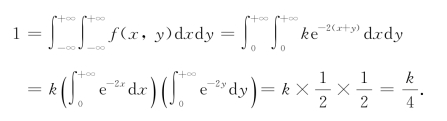
则k＝4.故有(www.xing528.com)

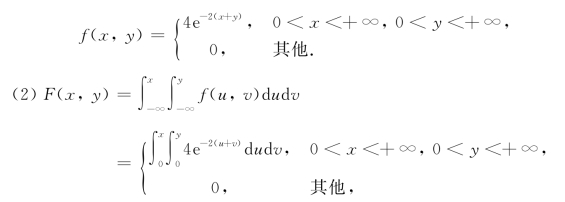
即

（3）由于

FX(x)＝F(x，＋∞)，

即

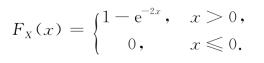
边缘密度函数

即

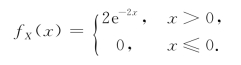
同理可得

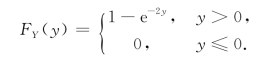
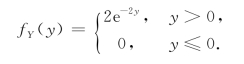
下面介绍两个常用的分布.

例4　设G为平面上的有界区域，面积为A，若二维随机变量（X，Y）的联合密度函数为

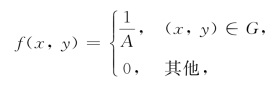
则称二维随机变量（X，Y）在G上服从均匀分布.

若区域G1是G内面积为A1的子区域，则有

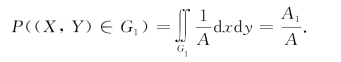
这表明概率只与G1的面积有关（成正比），而与G1在G内的位置无关，这正是均匀分布的“均匀”含义.

例5　设二维随机变量（X，Y）的联合密度函数为

f(x，y)＝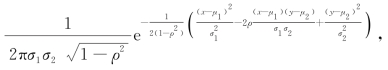

－∞＜x＜＋∞，－∞＜y＜＋∞，

其中，σ1＞0，σ2＞0，－1＜ρ＜1，则称二维随机变量（X，Y）服从参数为μ1，μ2，σ1，σ2，ρ的二维正态分布.记（X，Y）～N（μ1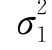，；μ2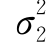，；ρ）.试求二维正态随机变量的边缘密度函数fX（x），fY（y）.

解　令

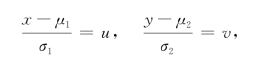
则

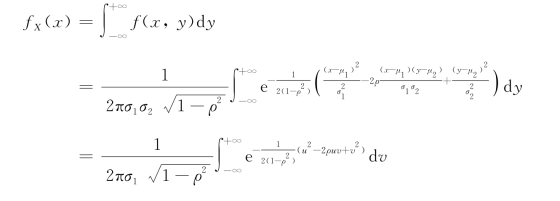
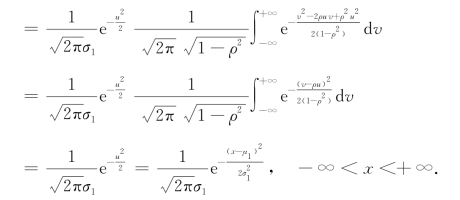
同理可得

由此可见二维正态分布N（μ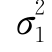，；μ2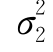，；ρ）的两个边缘分布均为一维正态分布，且X～N（μ1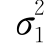，），Y～N（μ2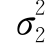，）.这两个一维正态分布均与ρ无关，说明ρ不同，得出的二维正态分布也不同，但其边缘分布却是相同的，所以边缘分布是不能唯一确定联合分布的.