《概率论与数理统计》中一、二维随机变量的分布

考察某地区儿童的体质情况，就要观察每个儿童的体重X和身长Y.如果样本空间Ω＝{ω}＝{某地区的全体儿童}，那就要同时观察X（ω），Y（ω），即要考查（X（ω），Y（ω）），这里X，Y均为随机变量.

定义1　设Ω为样本空间，X（ω），Y（ω）是Ω上的两个随机变量，则由它们构成的一个二维向量（X（ω），Y（ω））称为二维随机向量或二维随机变量，简记为（X，Y）.

对于二维随机变量（X，Y），若用FX（x），FY（y）分别表示X与Y的分布函数，则它们依次表示了事件{X≤x}和{Y≤y}的概率，即

FX(x)＝P(X≤x)， FY(y)＝P(Y≤y).

它们分别描述了随机变量X和Y的统计规律.然而，对于如下的交（积）事件

{X≤x}∩{Y≤y} 或记为 {X≤x，Y≤y}

的概率，却无法通过FX（x），FY（y）表示出来.这说明二维随机变量（X，Y）的性质不仅与X，Y有关，而且还依赖于这两个随机变量间的关系.因此，逐个地来研究X和Y的性质是不够的，而需将（X，Y）作为一个整体进行研究.同一维随机变量相类似，我们也借助“分布函数”来研究二维随机变量.

定义2　设（X，Y）是二维随机变量，x，y为任意实数，事件{X≤x，Y≤y}所对应的概率P{X≤x，Y≤y}是（x，y）的函数，则函数

F(x，y)＝P(X≤x，Y≤y)

称为二维随机变量（X，Y）的联合分布函数，简称分布函数.X，Y的分布函数FX（x），FY（y）称为（X，Y）关于X，Y的边缘分布函数.

由

{X≤x}＝{X≤x}∩{Y＜＋∞}＝{X≤x，Y＜＋∞}，

{Y≤y}＝{X＜＋∞}∩{Y≤y}＝{X＜＋∞，Y≤y}，

有

FX(x)＝P(X≤x)＝P(X≤x，Y＜＋∞)，

FY(y)＝P(Y≤y)＝P(X＜＋∞，Y≤y)，

从而得到联合分布函数和边缘分布函数的关系如下：

FX(x)＝F(x，＋∞)， FY(y)＝F(＋∞，y).

这就告诉我们，如果知道了联合分布函数，就可求出边缘分布函数.

若将二维随机变量（X，Y）看成是平面上随机点的坐标，则F（x，y）就是随机点（X，Y）落在以（x，y）为顶点，而位于该点左下方的无穷矩形内（图2.15所示的阴影部分）的概率.(www.xing528.com)

根据以上解释可以得到随机点（X，Y）落入矩形{x1＜X≤x2，y1＜Y≤y2}（图2.16所示的阴影部分）内的概率为

P(x1＜X≤x2，y1＜Y≤y2)

＝F(x2，y2)－F(x2，y1)＋F(x1，y1)－F(x1，y2).

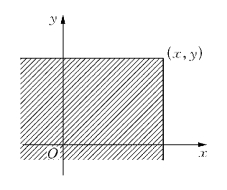
图2.15

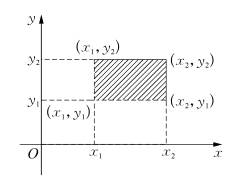
图2.16

联合分布函数F（x，y）具有如下性质：

（1）0≤F（x，y）≤1，且对于固定的x，

对于固定的y，

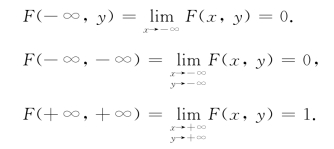
（2）F（x，y）是x或y的单调不减函数，即对任意固定的y，当x2＞x1时，F（x2，y）≥F（x1，y），对任意固定的x，当y2＞y1时，F（x，y2）≥F（x，y1）.

（3）F（x，y）关于x是右连续的，关于y也是右连续的，即

F(x，y)＝F(x＋0，y)， F(x，y)＝F(x，y＋0).

（4）对任意x1＜x2，y1＜y2，有

F(x2，y2)－F(x2，y1)＋F(x1，y1)－F(x1，y2)≥0.

若二元函数F（x，y）具有以上4个性质，即为某二维随机变量（X，Y）的分布函数.