1.均匀分布
设随机变量X的值只落在区间（a，b）内，其密度函数f（x）在（a，b）上为常数K，即
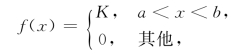
则称随机变量X在（a，b）上服从均匀分布.
由密度函数性质，有
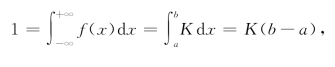
得
，从而有
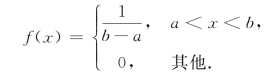
分布函数为
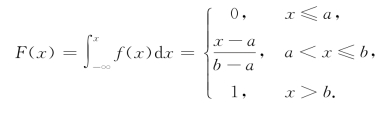
f（x），F（x）的图形分别如图2.6，2.7所示.
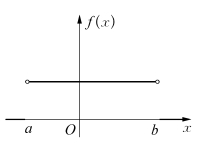
图2.6
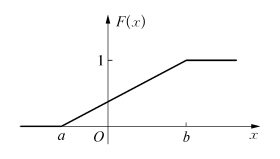
图2.7
当a＜x1＜x2＜b时，X落在区间（x1，x2）内的概率为
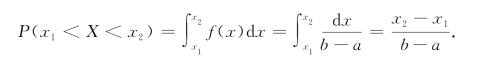
这表明服从均匀分布的随机变量X落在某区间（属于（a，b）内）内的概率只与此区间的长度成正比.也就是说，X落在（a，b）内任意等长度的区间内的可能性是一样的，这实际上也就是等可能概型的推广.
例4 设电阻R是一个均匀分布在900～1100Ω的随机变量，求R落在950～1000Ω之间的概率.
解 由题意可得R的密度函数
所求概率为
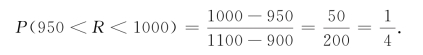
2.指数分布
设随机变量X的密度函数为
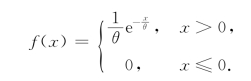
式中，θ＞0，则称随机变量X服从参数为θ的指数分布.
在有些教材中，也将指数分布的密度函数写成
式中，λ＞0.可以看出
.本书一般采用θ作为参数.
由式（2.5）可得X的分布函数为
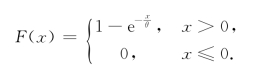
f（x）与F（x）的图形分别如图2.8、2.9所示.
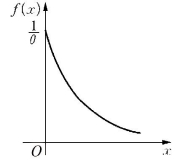
图2.8
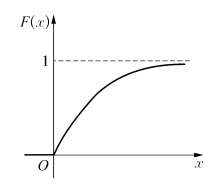
图2.9
指数分布有重要应用，常用它来作为各种“寿命”分布的近似，例如无线电元件的寿命，动物的寿命，电话问题中的通话时间，随机服务系统中的服务时间等都常假定服从指数分布.
指数分布的重要性还表现在它具有“无记忆性”.设随机变量X服从参数为θ的指数分布，则有
P(X＞x0＋x|X＞x0)＝P(X＞x).
事实上
“无记忆性”的实际意义是，一个寿命服从指数分布的电子元件，如果我们在某个x0时刻检查该电子元件，发现它是好的（即各项指标均达到规定要求），那么在这个条件下，从x0时刻开始它的寿命分布将和没有使用时完全一样，即可当作新的元件.因此人们也风趣地称指数分布为“永远年轻”的分布.
3.正态分布
设随机变量X的密度函数为
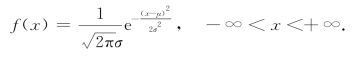
式中，μ，σ＞0为常数，则称随机变量X服从参数为μ、σ的正态分布或高斯（Carl Friedrich Gauss，1777—1855）分布，记为X～N（μ，σ2）.
f（x）确是一个密度函数，因为它满足
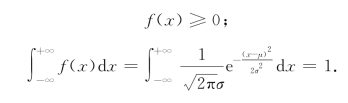
事实上，作变换
，则
作极坐标变换
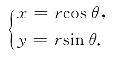
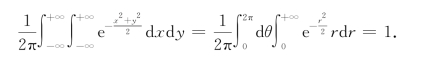
又因
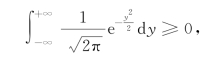
故得
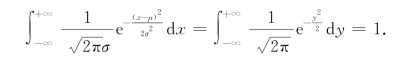
f（x）的图形如图2.10所示.f（x）具有如下性质：
（1）f（x）的图形是关于x＝μ对称的；
（2）当x＝μ时，
为最大值；
（3）f（x）以x轴为渐近线.
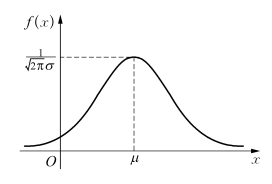
图2.10
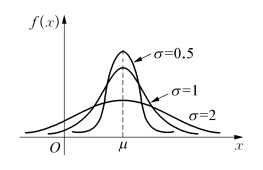
图2.11
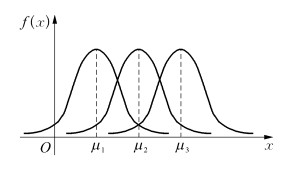
如图2.11，如果固定μ，改变σ，则当σ较大时，图形比较低而平坦；当σ较小时，图形比较高而峻峭.
如图2.12，如果固定σ，改变μ，则图形沿x轴平移，而不改变其形状.
(www.xing528.com)
图2.12
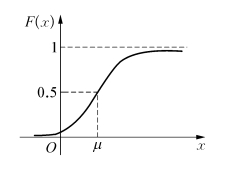
图2.13
若X～N（μ，σ2），则X的分布函数为
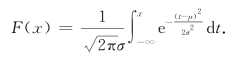
图形如图2.13所示.
参数μ＝0，σ＝1时的正态分布称为标准正态分布，记为X～N（0，1），其密度函数记为
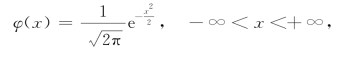
分布函数为
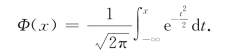
Φ（x）的函数值，已编制成表可供查用，见附表2.查表方法是，先看附表2第一列，找到x的整数部分和小数点后第1位；再看附表2第一行，找到x的小数点后第2位；然后在表中行列交叉点处查得Φ（x）的值.
当x＜0时，可由
来求Φ（x）的值.
因为
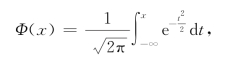
令t＝－u，
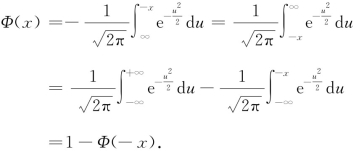
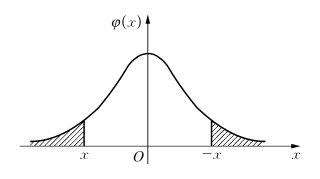
图2.14
或者由Φ（x）的几何意义，从图2.14亦可直接得出式（2.7）.
例5 设X～N（0，1），求P（－∞＜X＜－3），P（|X|＜3）.
解 P（－∞＜X＜－3）＝Φ（－3）＝1－Φ（3）
＝1－0.9987＝0.0013.
P(|X|＜3)＝P(－3＜X＜3)
＝Φ(3)－Φ(－3)＝Φ(3)－(1－Φ(3))
＝2Φ(3)－1＝2×0.9987－1＝0.9974.
对X～N（μ，σ2），求概率的关键是要会计算X的分布函数F（x）的值.下面我们可以通过变换将F（x）的计算转化为Φ（x）的计算，而Φ（x）的值是可以通过查表得到的.
事实上若令
＝y，则有
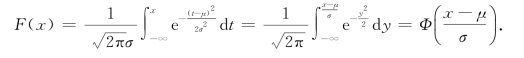
可得
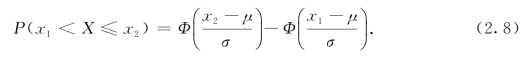
例6 设X～N（1，4），求P（5＜X≤7.2），P（0＜X≤1.6）.
解 根据式（2.8）有
P(5＜X≤7.2)＝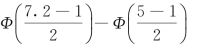
＝Φ(3.1)－Φ(2)
＝0.9990－0.9772
＝0.0218.
P(0＜X≤1.6)＝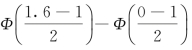
＝Φ(0.3)－Φ(－0.5)
＝Φ(0.3)＋Φ(0.5)－1
＝0.6179＋0.6915－1
＝0.3094.
例7 设X～N（μ，σ2），求P（|X－μ|＜3σ）.
解 P（|X－μ|＜3σ）＝P（μ－3σ＜X＜μ＋3σ）
＝
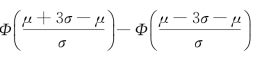
＝Φ(3)－Φ(－3)
＝2Φ(3)－1
＝2×0.9987－1
＝0.9974.
可见一次试验里X落入区间（μ－3σ，μ＋3σ）内的概率为0.9974，即X几乎必然落在上述区间内，这就是通常所谓“3σ”原理.
正态分布是概率论中最重要的一种分布，因为它是自然界中最常见的一种分布.理论上已证明了，如果某个数量指标呈现随机性是由很多随机因素影响的结果，而每个随机因素的影响又都不太大，这时数量指标就服从正态分布.例如，测量误差、炮弹弹着点分布、人的体重、产品的尺寸、农作物收获量等均可作为正态分布来研究.另外，正态分布具有良好的性质，理论上研究得比较透彻，许多其他分布常可用正态分布近似.这就使得概率论基本上是围绕正态分布发展起来的.
例8 某人需乘车前往某地，现有两条路线可供选择.第一条路线较短，但交通比较拥挤，到达机场所需时间X（单位为分钟）服从正态分布N（50，100）.第二条路线较长，但出现意外的阻塞较少，所需时间X服从正态分布N（60，16）.（1）若有70分钟可用，问应走哪一条路线？（2）若有65分钟可用，又应选择哪一条路线？
解 在规定时间内，哪条路线到达目的地的概率大就选哪一条路线.（1）有70分钟可用：
走第一条路线，及时赶到目的地的概率为
P(0＜X≤70)＝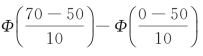
＝Φ(2)－Φ(－5)≈Φ(2)，
走第二条路线，及时赶到目的地的概率为
P(0＜X≤70)＝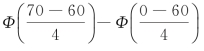
＝Φ(2.5)－Φ(－15)≈Φ(2.5).
由于Φ（2.5）＞Φ（2），所以选择第二条路线.
（2）有65分钟可用：
走第一条路线，及时赶到目的地的概率为
P(0＜X≤65)＝
Φ(1.5)，
走第二条路线，及时赶到目的地的概率为
P(0＜X≤65)＝
≈Φ(1.25).
由于Φ（1.5）＞Φ（1.25），所以选择第一条路线.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
