【摘要】：定义2设F（x）是随机变量X的分布函数，若存在非负函数f（x），对任意实数x，有则称X为连续型随机变量.f（x）称为X的概率密度函数或密度函数.f（x）的图形是一条曲线，称为密度（分布）曲线.由式（2.5）可知，连续型随机变量的分布函数F（x）是连续函数.F（x）的几何意义，由式（2.5）可知，表示在点x左面，密度曲线f（x）下面所围图形的面积，如图2.3所示.密度函数具有下面四个性质：(1)f
定义2 设连续型随机变量X的密度函数为f（x），若积分
绝对收敛，则称这个积分值为X的数学期望或平均值，简称期望或均值，记为E（X），即
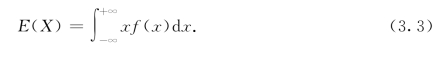
若积分
不绝对收敛，则称X的期望不存在.
E（X）的物理意义，可理解为以质量密度为f（x）的一维质点系的重心.
例5 设随机变量X服从密度函数为
的柯西分布，试证X的期望不存在.
解 由于
即
不绝对收敛，故E（x）不存在.
例6 设随机变量X服从均匀分布，其密度函数为
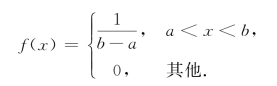
求E（X）.(www.xing528.com)
解 
例7 设随机变量X服从指数分布，其密度函数为
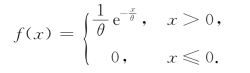
其中，θ＞0，求E（X）.
解 
＝
＝－
例8 设随机变量X服从正态分布，其密度函数为
求E（X）.
解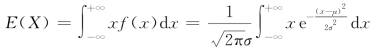 
＝
＝
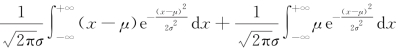
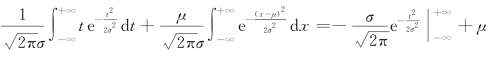
＝μ.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
