概率论与数理统计中的非离散型随机变量及其分布函数

上一节介绍了离散型随机变量，它的取值是有限个或可列无穷多个，这一点表现出离散随机变量的局限性.实际上，另有一些随机变量，它的取值是充满整个区间的，例如，测试某地一天的气温，已知其变化范围是从－5℃到8℃，那么气温T是一随机变量，它的取值充满区间[－5，8]；又如测试灯泡寿命试验中的灯泡寿命Y也是一个随机变量，它在区间[0，＋∞）上取值.T与Y均是非离散型随机变量.由于这种随机变量可能取的值不可能一个一个地列举出来，所以就不可能像离散型随机变量那样用分布律来描述它们的分布.又因为我们所遇到的非离散型随机变量通常取任一指定实数值的概率都等于0（这个结果今后我们可从理论上加以证明）.例如，上述灯泡的寿命Y是一个随机变量，事件{Y＝y0}表示灯泡寿命正好是y0.但我们即使用许许多多灯泡去作寿命试验，恐怕也没有一个灯泡能正好在指定的时刻寿命结束，使寿命恰好为y0，这说明事件{Y＝y0}的频率在零附近波动，自然P（Y＝y0）＝0.因而，对这样的随机变量X我们不再关心它取某一特定值的概率，转而去研究它所取的值落在某一个区间（x1，x2]内的概率P（x1＜X≤x2）.又由于

所以只要知道P（X≤x2）和P（X≤x1）就可以求出P（x1＜X≤x2）.这就是说，如果对任一个数x能知道P（X≤x），则随机变量X落在任一区间的概率可通过式（2.3）算出.因此，我们用P（X≤x）来表示X取值的可能性.

定义1　设X为随机变量，x是任意实数，则函数

F(x)＝P(X≤x)

称为随机变量X的分布函数.

由定义1可知，分布函数是个普通的实函数，它的定义域是（－∞，＋∞），值域是区间[0，1].分布函数在x处的值就是随机变量X的值落在区间（－∞，x]内的概率.

有了X的分布函数，我们就可以用

计算出X落入区间（x1，x2]的概率.也就是说，分布函数完整地描述了随机变量X随机取值的统计规律性.

例1　已知X的分布律为

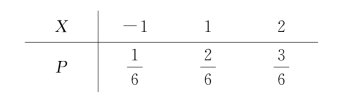
求：（1）X的分布函数；（2）

解　（1）根据X的分布律，当x＜－1时，{X≤x}是不可能事件，所以

F(x)＝0；

当－1≤x＜1时，{X≤x}＝{X＝－1}，所以

F(x)＝P(X≤x)＝P(X＝－1)＝；

当1≤x＜2时，有{X≤x}＝{X＝－1}∪{X＝1}，所以

F(x)＝P(X≤x)＝P(X＝－1)＋P(X＝1)＝；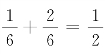

当x≥2时，{X≤x}是必然事件，所以

F(x)＝1.

综上所述，

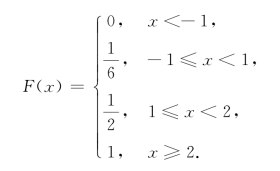
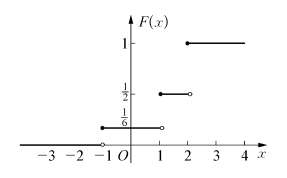
图2.1

F（x）的图形如图2.1所示.它是一条阶梯形曲线，在x＝－1，1，2处间断.

(2)

(3)

＝(P(X＝－1)＋P(X＝1))－(P(X＝－1)＋P(X＝1))

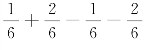＝＝0.

此例告诉我们，求离散型随机变量的分布函数，可用公式

此例说明，虽然分布函数概念比较重要，但对离散型随机变量来说，还是用分布律描述其取值规律比较方便.(https://www.xing528.com)

分布函数具有如下性质：

(1)0≤F(x)≤1，－∞＜x＜∞；

（2）F（x）是单调不减的函数，即x1＜x2时，有

F(x1)≤F(x2)；

(3)；

（4）F（x＋0）＝F（x），即F（x）是右连续的.

下面是取值充满一个区间的随机变量的例子.

例2　一靶子是一个半径为2米的圆盘.设击中靶上任一同心圆盘的概率与该圆盘的面积成正比，并设射击均能中靶.以X表示弹着点与圆心的距离，求随机变量X的分布函数F（x）及概率P（0.5＜X≤1）.

解　当x＜0时，{X≤x}是不可能事件，故有

F(x)＝P(X≤x)＝0.

当0≤x＜2时，由题意有

P(0≤X≤x)＝kx 2，

k为比例系数.由于{0≤X≤2}是必然事件，有

1＝P(0≤X≤2)＝k×22，

解得k＝，即P（0≤X≤x）＝.于是

F(x)＝P(X≤x)＝P((X＜0)∪(0≤X≤x))

＝P(X＜0)＋P(0≤X≤x)＝0＋.

当x≥2时，（X≤x）是必然事件，故

F(x)＝P(X≤x)＝1.

综上所述，得

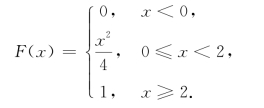
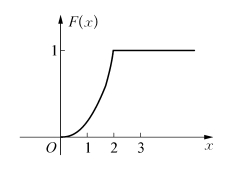
图2.2

图形见图2.2，它是一条连续曲线.

所求概率为

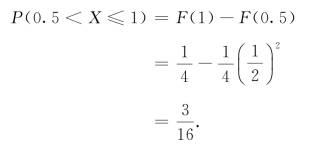
在这个例子中，若令

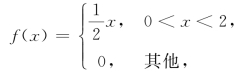
显然有

这种分布函数F（x）能用一个非负可积函数f（x）的变上限积分表示，则称X为连续型随机变量.连续型随机变量是我们今后主要的研究对象.