泊松分布的理论和应用

设随机变量X的分布律为

则称随机变量X服从参数为λ的泊松（Siméon Denis Poisson，1781—1840）分布，记为X～π（λ）.容易验证，满足条件

(1)P(X＝k)＝≥0，k＝0，1，2，…，

(2)

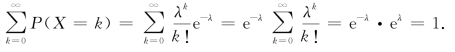
泊松分布在理论和应用上都是很重要的.许多随机变量都近似地服从泊松分布.例如，飞机被炮弹击中的中弹数、来到公共汽车站的乘客数、机床发生故障的次数、自动控制系统中元件损坏的个数、某商店中来到的顾客人数等，均近似地服从泊松分布.

对于服从二项分布的随机变量，在计算概率时，可以利用泊松分布来给出近似值.

定理1　设随机变量Xn，n＝1，2，…服从参数为n、pn的二项分布，即有

若满足＝λ＞0，则有

证　记λn＝npn，则

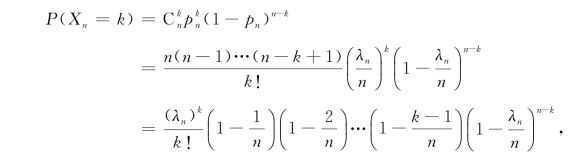
对于固定的k有

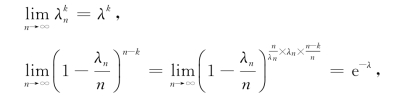
及(www.xing528.com)

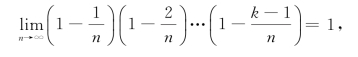
故有

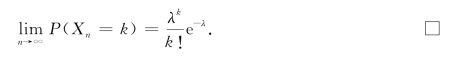
在实际应用中，当n很大，p很小时，二项分布就可用泊松分布来近似地表示

其中λ＝np.这也就是计算二项分布的近似公式.计算泊松分布有表可查.

例5　为了保证设备正常工作，需要配备适当数量的维修工人.现有同类型设备300台，各台的工作是相互独立的，发生故障的概率都是0.01.如果一个工人同时只能修理一台发生故障的设备，问至少需要配备多少工人，才能保证当设备发生故障而不能及时修理的概率不大于0.01？

解　设需配备N个修理工，300台设备同一时刻发生故障的设备台数为X，则X服从参数n＝300，p＝0.01的二项分布，即X～B（300，0.01）.设备发生故障而无人修理的事件为{X＞N}.由题意得

P(X＞N)≤0.01，

即

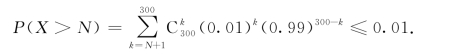
要由上式求出最小的N，当然是困难的.由n较大，p较小，可以用式（2.2）作近似计算，这时λ＝np＝3，故有

P(X＞N)＝1－P(X≤N)

≈1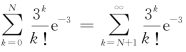－≤0.01.

查附表3可得最小的N＝8.所以配备8个修理工就能达到要求.