伯努利概型二项概率公式简介

随机现象的规律性只有在相同条件下进行大量重复试验或观察才能表现出来.将一个试验重复独立地进行n次，这是最基本最重要的一种具有独立性试验的模型，下面给出一般的定义.

定义5　我们作了n次试验，且满足

（1）每次试验只有两种可能结果，A发生或不发生；

（2）n次试验是重复进行的，即A发生的概率每次均一样；

（3）每次试验是独立的，即每次试验A发生与否与其他次试验A发生与否是互不影响的.

这种试验称为伯努利（Jacob Bernoulli，1654—1705）概型，或称为n重伯努利试验.

在n重伯努利试验中，我们特别感兴趣的是事件A发生的次数，用p表示每次试验A发生的概率，则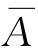发生的概率为1－p＝q，用Pn（k）表示n重伯努利试验中A出现k，0≤k≤n次的概率，下面就来推出计算Pn（k）的公式.

由于事件A在指定的某k次试验中发生，而在其余（n－k）次试验中不发生的概率为p k（1－p）n－k.在n次试验中，由于事件A发生k次可以有各种排列顺序，由排列组合知识可知它共有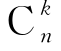种，而这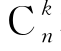种排列所对应的个事件显然是互不相容的，故由加法定理可得

这就是n重伯努利试验中A出现k次的概率计算公式.由于，k＝0，1，2，…，n正好是（（1－p）＋p）n按二项式公式展开时的各项，所以上述公式称为二项概率公式.

例12　为了摧毁某个目标，只要命中两次就够了.已知每次射击的命中率为0.8，问独立地连续射击5次摧毁目标的可能性有多大？

解　设A表示射击5次至少命中2次的事件，Ai表示射击5次恰好命中i次的事件，i＝0，1，2，3，4，5，则

＝A0∪A1.

由加法定理有(www.xing528.com)

P(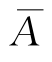)＝P(A0)＋P(A1).

由二项概率公式有

P(A0)＝P5(0)＝(0.2)5＝0.00032，

P(A1)＝P5(1)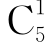＝×0.8×(0.2)4＝0.0064.

故所求概率为

P(A)＝1－P(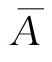)＝1－(0.00032＋0.0064)＝0.99.

例13　设某工厂生产的产品出现次品的概率为0.005，现从中任取1000件产品，问其中有次品的概率是多少？

解　可视为n＝1000，p＝0.005，q＝0.995的伯努利试验，利用逆事件得所求事件的概率为

P＝1－P1000(0)＝1－(0.995)1000＝0.9933.

在本题中，我们假定产品中的次品数是已知的，然后根据它来计算种种概率.而在实际问题中，情况恰恰相反，次品数是未知的，并且正是我们希望通过抽样检验来确定的.一般认为，抽出来的样本的质量情况在某种程度上反映了整批产品的质量情况.例如，如果整批产品中次品很多，则抽查的样本中含有次品的可能性就相当大；反之，若产品中次品极少，则从中抽查一、两只样本而得到次品的可能性就很小，因而样本中所含次品数的多少就为我们估计整批产品中的次品数提供了某种根据.例如为了确定某批产品的次品率，通常采用的方法是从这批产品中抽若干个产品作为样本来检验，并用样本的次品率来估计整批产品的次品率，关于这个课题的研究，构成了数理统计的重要内容.

由于抽样带有随机性，因而不同的抽样可能得到不同的结果，所以我们有必要对各种结果出现的可能性大小进行讨论，这为我们根据样本情况推断整批产品情况提供了理论依据，这种研究是概率论的任务.从这里也看出，概率论与数理统计有着很密切的联系.