事件的相互独立性-《概率论与数理统计》相关原理

我们已经知道，条件概率P（A|B）和概率P（A）一般情况下是不等的，这说明事件B的发生对事件A发生的概率是有影响的.但在某些情况下，如袋中有a只白球，b只黑球，在有放回摸球的试验中，设B表示第一次摸得白球的事件，A为第二次摸得白球的事件，则有P（A|B）＝P（A），即B发生与否对A的发生没有影响.这种现象在概率论里称为独立性，概率论中相当一部分内容都是围绕它讨论的，为此，我们给出

定义2　设事件A，B满足

P(AB)＝P(A)P(B)，

则称事件A，B是相互独立的.

由定义2，我们可知必然事件Ω和不可能事件∅与任何事件都相互独立.

若事件A，B相互独立，且P（B）＞0，则有

所以这与我们前面所理解的独立性是一致的.

若事件A，B相互独立，则可得到与B、A与与也都相互独立.

事实上，由B＝B－A＝B－AB，有

P(B)＝P(B－AB)＝P(B)－P(AB)＝P(B)－P(A)P(B)

＝P(B)[1－P(A)]＝P(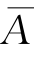)P(B)，

故得与B相互独立，至于A与与的独立性，可类似推得.

在实际问题中，常常不是根据定义来判断事件的独立性，而是由独立性的实际含义，即一个事件发生并不影响另一个事件发生的概率来判断两事件的相互独立性.

例5　甲、乙两射手独立地射击同一目标，他们击中目标的概率分别为0.9与0.8.求在一次射击中（每人各射一次）目标被击中的概率.

解　设C为目标被击中，A为甲射中目标，B为乙射中目标.由，且根据独立性有

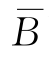P()＝P(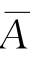)＝P()P()

＝(1－0.9)×(1－0.8)＝0.1×0.2＝0.02，

故所求概率为

P(C)＝1－P(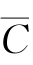)＝1－0.02＝0.98.

在概率论的实际应用中，只有两个事件的独立性是不够的，还必须用到多个事件的独立性.下面先讲三个事件的独立性，然后再讲一般的情形.

定义3　对于三个事件A，B，C，若

4个等式同时成立，则称A，B，C是相互独立的.

应该指出的是，由式（1.3）不能推得式（1.4），反之由式（1.4）也不能推得式（1.3），必须同时满足才称A，B，C相互独立.

式（1.3）成立只表明A，B，C中任意两个事件均独立，故又称两两独立.由定义知，若A，B，C相互独立，则必两两独立.

定义4　对n个事件A1，A2，…，An，如果对于任意k个自然数i1，i2，…，ik，1≤i1＜i2＜…＜ik≤n，2≤k≤n都有

则称事件A1，A2，…，An相互独立.

若A1，A2，…，An相互独立，则将A1，A2，…，An中的任意多个事件换成它们的逆事件，所得的n个事件仍然相互独立.

要根据定义来判断多个事件是否独立，是相当麻烦的.因此，对于实际问题不是根据定义，而是根据经验进行直观的判断，如许多门大炮各自互不影响地向目标射击一次，则各炮射中目标就可认为是相互独立的.在计算若干事件同时发生的概率时，若这些事件是相互独立的，则概率计算可大大简化.

相互独立事件至少发生一个的概率计算公式：(www.xing528.com)

设A1，A2，…，An相互独立，则

因为

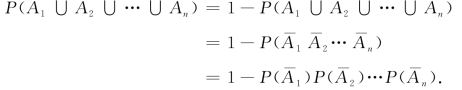
例6　设某类型的高炮每次击中飞机的概率为0.2，问至少需要多少门这样的高炮同时独立发射（每门射一次）才能使击中飞机的概率达到95%以上.

解　设n为所需的高炮门数，A为击中飞机的事件，Ai为第i门炮击中飞机的事件，i＝1，2，…，n.现求n使得

P(A)＝P(A1∪A2∪…∪An)≥0.95.

由式（1.5）得

P(A)＝1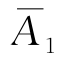－P(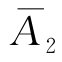)P()…P()＝1－(1－0.2)n，

解不等式

1－(1－0.2)n≥0.95，

即

0.8n≤0.05， n lg 0.8＜lg 0.05，

得

n≥14.

故至少要14门高炮才能有95%以上的把握击中飞机.

例7　称一只元件能正常工作的概率p为这只元件的可靠性；称由元件组成的系统能正常工作的概率为这个系统的可靠性.求图1.4、1.5所示两个系统的可靠性，假设其中每只元件的可靠性均为r（0＜r＜1），且各元件能否正常工作是相互独立的.

系统I（串联情况）

图1.4

系统II（并联情况）

图1.5

解　设Ai表示“第i只元件能正常工作”，i＝1，2，3，则A1 A2 A3表示“系统I能正常工作”，A1∪A2∪A3表示“系统II能正常工作”.

系统I的可靠性为

P(A1 A2 A3)＝P(A1)P(A2)P(A3)＝r 3.

系统II的可靠性为

由于

P(A1∪A2∪A3)－P(A1 A2 A3)＝(1－(1－r)3)－r 3

＝3r－3r 2＝3r(1－r)≥0，

故虽然系统I、系统II同样由三只元件组成，但系统II的构成方式的可靠度比系统I的构成方式的可靠度来得大.