概率计算方法及等可能概型介绍

前面我们从某些事件的概率出发，利用概率的性质计算出了一些事件的概率.但对于等可能概型（又称古典概型），我们却可以直接计算任意事件的概率.所谓等可能概型是指在这种试验中，样本空间仅包含有限个基本事件，并且每个基本事件的发生是等可能的，即这种试验应满足：

(1)Ω＝{ω1，ω2，…，ωn}；

(2)P(ω1)＝P(ω2)＝…＝P(ωn).

由于基本事件是互不相容的，从而有

1＝P(Ω)＝P({ω1}∪{ω2}∪…∪{ωn})

＝P(ω1)＋P(ω2)＋…＋P(ωn).

由（2）可得

设任一事件A，它是由组成的，则有

以上是事件A的概率计算公式，即概率的古典定义.它告诉我们对于等可能概型，计算事件概率关键在于计算基本事件总数和该事件所包含的基本事件数.可是由于样本空间的设计可有各种不同的方法，这就使得等可能概型的计算变得花样繁多，难易程度也就大不相同了.

一般我们把从有限个元素中随机抽取的问题当作是等可能的，今后不再加以说明.

例2　一只袋中装有五只大小相同的球，其中三只白色，两只黑色.现从袋中取球两次，每次一只，取出后不再放回袋中.试求：

（1）两只球都是白色的概率；

（2）两只球颜色不同的概率；

（3）至少有一只白球的概率.

解　设A为两只球都是白色的事件，B为两只球颜色不同的事件，C为至少有一只白球的事件.根据第一节例5，样本空间Ω所含基本事件总数n＝20，事件A所含基本事件数kA＝6，事件B所含基本事件数kB＝12，事件C所含基本事件数kC＝18，则事件A，B，C的概率分别为

为了计算有关事件的概率，首先我们应设计样本空间，然后将基本事件总数计算出来.一般来说，我们无需将样本空间中的基本事件一一列出来，而是利用排列、组合及加法原理、乘法原理等知识把基本事件总数、所求事件所包含的基本事件数直接计算出来，进而求出所求事件的概率.

在例2中，可直接得到n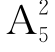＝＝5×4＝20，A所包含的基本事件数kA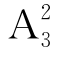＝＝3×2＝6，B所包含的基本事件数C所包含的基本事件数可以用所包含的基本事件数来帮助计算.

事实上，是表示两只球均为黑色的事件，故有.于是kC＝n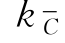－＝18.当然，也可以由

C＝{（第一只白球，第二只黑球）}∪{（第一只黑球，第二只白球）}∪{（两只都是白球）}，

得

应特别注意的是，为了解决问题方便，样本空间可以作不同设计，但必须保持等可能性的要求，否则就不能利用等可能概型来求概率.如在例2中若视白色球间是无区别的，黑色球间也是无区别的（见第一节例5），可得

Ω＝{（白，白），（白，黑），（黑，白），（黑，黑）}，

这就破坏了等可能性.

例3　袋中有a只白球，b只黑球，依次将球一只只摸出，不放回，求第k次摸出白球的概率（1≤k≤a＋b）.

解　设想将球编号，一只只摸出直至第k个球取出为止，则基本事件总数就是从a＋b个编号的球中选出k个球进行排列的排列个数，即.

又设A为第k次摸出白球的事件.要使A发生只需从a只白球中选出一只放在第k个位置上作为第k次摸出的球，而前面k－1个位置可以任意放余下各球，由乘法原理得

故有

本题也可给出另一解法.设想将a＋b只球进行编号，每次试验将摸出的球顺次排列在a＋b个位置上，基本事件总数为n＝（a＋b）！，kA＝（a＋b－1）！a，故有

本题虽然是求第k次摸到白球的概率，然而结果却与k无关，即与摸球的次序无关，摸到白球的概率总是.对于在体育比赛或其他活动中进行的抽签，以上结果表明与抽签先后无关，机会是均等的.这当然与我们日常生活的经验是一致的.

如果将本问题改动一下，即每次取出一球记录下颜色后，又将其放回袋中.如此继续摸取，求第k次摸出白色球的概率.这种抽取方法称为放回抽样（前面的抽取方法称为不放回抽样）.这时抽取k只球的结果作为一个基本事件，则基本事件总数为（a＋b）k.这是由于第一次抽取一只球有（a＋b）种可能，第二次抽取一只球仍有（a＋b）种可能……所以基本事件总数为（a＋b）k.对于第k次摸出白球的事件A所包含的基本事件数，类似可得为（a＋b）k－1a.故有(www.xing528.com)

例4　某批产品有a件合格品，b件次品.从中用有放回和不放回两种抽样方式抽取n件产品，求恰有k件次品的概率.

解　（1）放回抽样：

从（a＋b）件产品中，有放回地抽取n件产品，所有可能的取法有（a＋b）n种.再来计算取出的n件产品中恰有k件次品的取法总数.对取出的n件产品，其中有k件次品，而k件次品可以出现在不同位置，所有可能的取法有种.对于取定的一种位置，这时由于取正品有a种可能，取次品有b种可能，故有a n－kb k种可能，所以取出的n件产品中恰有k件次品的取法有种.所求概率

（2）不放回抽样：

从（a＋b）件产品中取出n件产品（不计次序），所有可能取法有种.取出的n件产品中恰有k件次品的取法有种，这是因为k件次品可由b件次品中取出，有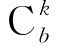种取法，（n－k）件正品可由a件正品中取出，有种取法.故所求概率为

并且P1≠P2.

例5　设有n个颜色互不相同的球，每只球都以等可能落入N（n≤N）只盒子中的任意一只盒子里.并假设每只盒子能容纳的球数是没有限制的.试求下列事件的概率：

A＝{某指定的一只盒子中没有球}，　　　

B＝{某指定的n只盒子中各有一只球}，　　

C＝{恰有n只盒子中各有一只球}，　　　　

D＝{某指定的一只盒子中恰有m只球}（m≤n）.

解　由于每只球落于N只盒子中均有N种可能，故基本事件总数为N n.也相当于从N个元素中选取n个的重复排列数.下面再分别求出每个事件所包含的基本事件数.

对事件A，可设想将指定的一只盒子去掉，可得kA＝（N－1）n.故有

对事件B，n只球落于指定的n只盒子里，每只盒子只有一只球，可得kB＝n！.故有

对于事件C，n只球落于指定的n只盒子里，每只盒子里只有一只球有n！种可能.现n只盒子未指定，可从N只盒子中任取n只盒子，有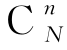种可能，可得.故有

对事件D，从n只球中任选m只球落于指定的一只盒子里有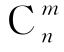种可能，再将余下的（n－m）只球任意落于（N－1）只盒子里有（N－1）n－m种可能，可得kD＝.故有

上面的问题也称为球在盒中的分布问题.事实上，有好些问题可以归结为球在盒中的分布问题，只不过在处理具体问题时，应分清问题中什么是“球”，什么是“盒”，不可颠倒.

例如，有n个人（n≤365），设每人的生日在一年365天中任一天的可能性是相等的.试求下列事件的概率：

A＝{n个人的生日均不相同}，

B＝{至少有一人的生日是元旦}.

对以上问题即可视人为“球”，365天可视为365只“盒子”.这样就可归结为球在盒中的分布问题了.故得

例6　从1～2000中任意取一整数，求取到的整数能被6或8整除的概率.

解　设A为取到的数能被6整除的事件，B为取到的数能被8整除的事件，则取出的数能被6或8整除的事件为A∪B，所求概率为

P(A∪B)＝P(A)＋P(B)－P(AB).

现基本事件总数为2000.由

得kA＝333，kB＝250，所以

同时能被6和8整除的数，也就是同时能被24整除的数，由

得kAB＝83，所以

所求概率为