概率论与数理统计：概率的定义及性质

设Ω为样本空间，对每一个事件A都有一个实数P（A），若满足下列三个条件：

(1)0≤P(A)≤1；

(2)P(Ω)＝1；

（3）对于两两互不相容的事件A1，A2，…有

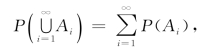
则称P（A）为事件A的概率.

条件（3）常称为可列（完全）可加性，也称为加法定理.

由概率的定义可以得到概率的如下性质.

性质1　不可能事件的概率为零，即P（∅）＝0.

证　因为

Ω＝Ω∪∅∪…，

所以

P(Ω)＝P(Ω)＋P(∅)＋…，

故

P(∅)＝0.　　　　　　　　□

性质2　概率具有有限可加性，即若事件A1，A2，…，An两两互不相容，则

P(A1∪A2∪…∪An)＝P(A1)＋P(A2)＋…＋P(An).

证　因为

A1∪A2∪…∪An＝A1∪A2∪…∪An∪∅∪∅∪…，

由可列可加性及性质1有

P(A1∪A2∪…∪An)＝P(A1)＋P(A2)＋…＋P(An).　　　　　　　　□

性质3　对任何事件A有

P(A)＝1－P().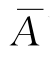

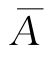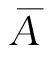证　由A∪＝Ω，A∩＝∅，故得

1＝P(A∪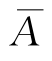)＝P(A)＋P().

将P（）移至等号左端即得

P(A)＝1－P().　　　　　　　　□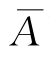

性质4 对事件A，B，若有A⊂B，则有

P(B－A)＝P(B)－P(A)

及

P(A)≤P(B).

图1.2

证　由图1.2可知

B＝A∪(B－A)

及

A∩(B－A)＝∅，

故有

P(B)＝P(A)＋P(B－A)，

即

P(B－A)＝P(B)－P(A).

由P（B－A）≥0，可得(www.xing528.com)

P(A)≤P(B).　　　　　　　　□

性质5　对任意两事件A，B有

P(A∪B)＝P(A)＋P(B)－P(AB).

证　由图1.3可知

A∪B＝A∪(B－A)

及

B＝AB∪(B－A)，

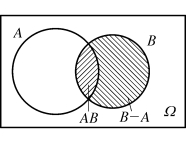
图1.3

而且

A∩(B－A)＝∅，

AB∩(B－A)＝∅，

故得

P(A∪B)＝P(A)＋P(B－A)

及

P(B)＝P(AB)＋P(B－A).

将上面两式相减，并将P（B）移到等号右边，即得

P(A∪B)＝P(A)＋P(B)－P(AB).　　　　　　　　□

性质5可推广到任意n个事件上去.例如当n＝3时，有

P(A1∪A2∪A3)

＝P(A1)＋P(A2)＋P(A3)－P(A1 A2)－P(A1A3)－P(A2 A3)＋P(A1 A2 A3).

例1　某人到武汉出差两天，据天气预报，第一天下雨的概率为0.6，第二天下雨的概率为0.3，两天都下雨的概率为0.1.求：

（1）第一天下雨而第二天不下雨的概率；

（2）第一天不下雨而第二天下雨的概率；

（3）至少有一天下雨的概率；

（4）两天都不下雨的概率.

解　设Ai为第i天下雨的事件，i＝1，2.由题意可知，P（A1）＝0.6，P（A2）＝0.3，P（A1 A2）＝0.1.

（1）设B为第一天下雨而第二天不下雨的事件，则有

B＝A1－A2＝A1－A1 A2，

且A1A2⊂A1，故得

P(B)＝P(A1－A1 A2)＝P(A1)－P(A1 A2)

＝0.6－0.1＝0.5.

（2）设C为第一天不下雨而第二天下雨的事件，用类似于（1）的解法有

P(C)＝P(A2－A1 A2)＝P(A2)－P(A1 A2)＝0.3－0.1＝0.2.

（3）设D为至少有一天下雨的事件，则有D＝A1∪A2，故得

P(D)＝P(A1∪A2)＝P(A1)＋P(A2)－P(A1A2)

＝0.6＋0.3－0.1＝0.8.

（4）设E为两天都不下雨的事件，则有

故得