随机事件及其运算-概率论与数理统计

概率论是研究随机现象数量规律的一门数学学科.对随机现象进行研究，就要进行观察、试验.为了叙述方便，我们把对自然现象或社会现象进行的观察或实验，都称为试验.如果一个试验在相同条件下重复进行，而每次试验的可能结果不止一个，但在进行一次试验之前却不能断言它出现哪个结果，则称这种试验为随机试验.以下所说的试验都是指随机试验.

在试验中，可能发生也可能不发生的事情，称为随机事件，简称事件.

例1　掷一枚硬币，出现正面及出现反面都是随机事件.

例2　掷一颗骰子，出现“1”点，“3”点，“5”点都是随机事件.

例3　电话接线员在上午8时到9时接到的电话呼叫次数，如出现0次，1次……及出现次数在20到50之间都是随机事件.

例4　对某一目标发射一发子弹，弹着点与目标中心的距离为0.1米，0.5米及0.2米到0.3米之间都是随机事件.

从上面的例子可以看出，在一个试验中，所出现的事件是很多的.例1的事件有两个，例2的事件有很多个，但却是有限的.例3和例4的事件却有无穷多个.

在一个试验下，不管事件有多少个，总可以从其中找出这样一组事件，它具有如下性质：

（1）每进行一次试验，必然发生且只能发生这一组中的一个事件；

（2）任何事件，都是由这一组中的部分事件组成的.

这样一组事件中的每一个事件称为基本事件，用ω来表示.基本事件的全体，称为试验的样本空间，用Ω表示.

在例1中，我们取

Ω＝{（出现正面），（出现反面）}.

在例2中，我们取

Ω＝{（出现1点），（出现2点），…，（出现6点）}.

在例3中，我们取

Ω＝{（出现0次），（出现1次），…}.

在例4中，我们取

Ω＝{（弹着点与目标中心的距离ω）|0≤ω＜＋∞}.

通常，Ω中的基本事件就是试验中所有可能直接出现的结果.根据这一点，我们可以对试验找出所有的基本事件.

如果我们把一个基本事件视为一个抽象的“点”，那么样本空间就是由这些抽象的“点”组成的空间.根据性质（2），一个事件就是由Ω中的部分点（基本事件）组成的集合.通常用大写字母A，B，C，…表示事件，它们是Ω的子集.

如果某个ω是事件A的组成部分，即这个ω在事件A中出现，记为ω∈A，读作ω属于A.如果在一次试验中所出现的ω有ω∈A，则称在这次试验中事件A发生.

如果ω不是事件A的组成部分，就记为ω∉A，读作ω不属于A.在一次试验中，所出现的ω有ω∉A，则称此试验A没有发生.

很显然，总有ω∈Ω，将Ω作为事件，则在试验中事件Ω总是发生的，故称Ω为必然事件.它不是随机事件，把它作为事件主要是为了讨论问题的方便.另一个不是随机事件而视为事件的就是不包含任何基本事件的事件，记为∅.由于对一切的ω有ω∉∅，故在试验中，∅总是不发生的，所以称∅为不可能事件.

如果我们有了一些事件，则可以从这些事件得出其他事件来，这就是事件的运算.下面先介绍事件的包含与等价关系，再讨论事件的运算.

如果事件A的组成部分也是事件B的组成部分，则称事件A包含于事件B，或称事件B包含事件A，记为A⊂B或B⊃A.A⊂B的直观意义就是如果事件A发生必有事件B发生.

如果同时有A⊂B，B⊂A，则称事件A与事件B等价，或称A等于B，记为A＝B.其直观意义是组成A、B的基本事件完全相同，因此可以看做是一样的.

将事件A与B的组成部分合并（A、B所共同的基本事件只取一次）而组成的事件称为事件A与事件B的并事件（或和事件），记为A∪B.由于A∪B发生是指属于A∪B的某个基本事件ω发生，所以ω不属于A就属于B，即表示不是A发生就是B发生，因而A∪B的直观意义就是A，B中至少有一个发生的事件.类似地，我们可以规定可列个事件A1，A2，…，Ai，…的并，记为

A1∪A2∪…∪Ai∪…， 或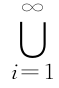Ai，

它表示A1，A2，…，Ai，…中至少有一个发生的事件.

事件A，B的共同组成部分所构成的事件，称为事件A与B的交事件（或积事件），记为A∩B.有时也可省去“∩”而简写为AB.若属于A∩B的某个ω发生，那就是A与B同时发生，所以A∩B的直观意义是A，B同时发生的事件.类似地，可以规定可列个事件A1，A2，…，Ai，…的交，记为

A1∩A2∩…∩Ai∩… 或 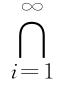A i，

它表示A1，A2，…，Ai，…同时发生的事件.

属于A而不属于B的部分所构成的事件，称为A与B的差事件，记为A－B，它表示A发生而B不发生的事件.

A∩B＝∅，则表示A与B不可能同时发生，称事件A与事件B互不相容.基本事件是互不相容的.

Ω－A称为事件A的逆事件，或称为A的对立事件，记为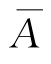.它表示A不发生的事件.这样可得

A∪＝Ω， A∩＝∅.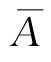

前一式表示A与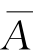至少有一个发生，后一式表示A与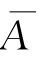不能同时发生.(www.xing528.com)

必须指出，直观意义能帮助我们理解事件间的关系，但不能代替严格的数学证明.下面我们来证明

我们首先证明

设，则有

从而可知，至少存在i0，使得，即.于是可知

这样就证明了式（1.1）.

其次，我们来证明

设，则至少存在i0，使得，即.于是可知

即.这样就证明了式（1.2）.

由式（1.1）、（1.2）同时成立，可知

以上是证明等价关系的一般方法.对于一些比较明显的等价关系，可以由直观意义获得，也可以借助几何直观获得.下面介绍文（John Venn，1834—1923）图.

用平面上的一个矩形表示样本空间Ω，矩形内的点表示基本事件ω，则事件间关系及运算就可用平面上的几何图形表示，如图1.1所示.事件A，B分别用两个小圆表示，阴影部分表示A与B的各种关系及运算.

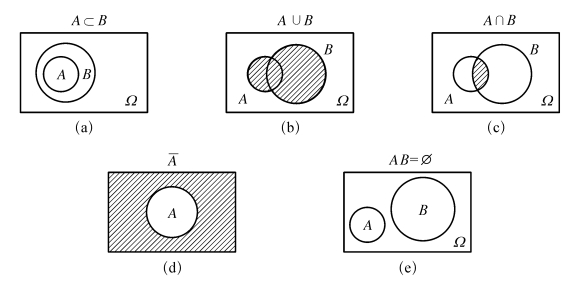
图1.1

由图1.1（c），可得

A－B＝A－AB，

(A－B)∪(B－A)＝(A∪B)－AB.

例5　一口袋中装有五只同样大小的球，其中三只是白色的，两只是黑色的.现从袋中取球两次，每次取一只，并且取出后不放回袋中.写出该试验的样本空间Ω.若A表示取到的两只球是白色的事件，B表示取到的两只球是黑色的事件，试用A，B表示下列事件：

（1）两只球是颜色相同的事件C；

（2）两只球是颜色不同的事件D；

（3）两只球中至少有一只白球的事件E.

解　假设每个球是可以区别的，则可以给每个球编上号：白1，白2，白3，黑4，黑5.于是有

Ω＝{（白1，白2），（白1，白3），（白1，黑4），（白1，黑5），（白2，白1），

（白2，白3），（白2，黑4），（白2，黑5），（白3，白1），（白3，白2），

（白3，黑4），（白3，黑5），（黑4，白1），（黑4，白2），（黑4，白3），

（黑4，黑5），（黑5，白1），（黑5，白2），（黑5，白3），（黑5，黑4）}.

从而，C＝A∪B，

若我们认为白球间是无区别的，黑球也是无区别的，则有

Ω＝{（白，白），（白，黑），（黑，白），（黑，黑）}.

这样C，D，E所表示的事件就更加简单了.

由这个例子可以看出，同一试验可以设计不同的样本空间，而设计的好坏取决于能否使讨论的问题得到简捷的解决.