直线与平面及两平面的相对位置可分为平行、相交和垂直(垂直是相交的特例)。
1.平行问题
1)直线与平面平行
直线与平面平行的几何条件:若直线平行于平面上一直线,则直线与该平面平行,如图2-53所示。
若直线平行于投影面垂直面,则该投影面垂直面具有积聚性的投影与直线的同面投影平行,如图2-54所示。
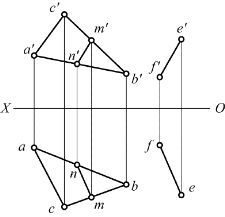
图2-53 直线与平面上一直线平行
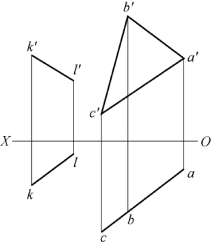
图2-54 直线与投影面垂直面平行
【例2-16】 已知直线KL∥△ABC,KL的正面投影k′l′和点K的水平投影k如图2-55(a)所示,求KL的水平投影kl。
分析:直线KL∥△ABC,在△ABC上任作一条直线,使之与KL平行,则这条直线的水平投影必与kl平行。
作图:过a′作a′d′∥k′l′,交b′c′于d′,按投影关系在bc上求出d,连接ad。过k作kl∥ad,与过l′所作的OX轴的垂线相交于l,如图2-55(b)所示,kl即为所求。
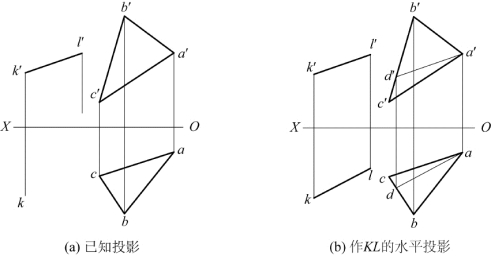
图2-55 作一和已知平面平行的直线的水平投影
【例2-17】 已知投影如图2-56(a)所示,过已知点K作一水平线KL与△ABC平行,求作KL的两面投影。
分析:在△ABC上作一水平线AD,过点K作直线KL∥AD,则直线KL的两面投影即为所求。
作图:过a′作a′d′∥OX,交b′c′于d′,按投影规律,在bc上求出d,过k′作k′l′∥OX,过k作kl∥ad,如图2-56(b)所示。
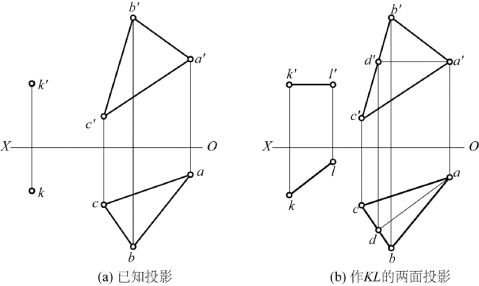
图2-56 作一和已知平面平行的水平线的两面投影
2)两平面平行
两平面平行的几何条件:若一平面上的两相交直线与另一平面上的两相交直线相互平行,则这两个平面相互平行,如图2-57所示。

图2-57 两平面上的相交直线相互平行
若两投影面垂直面相互平行,它们具有积聚性的那组投影相互平行,如图2-58所示。
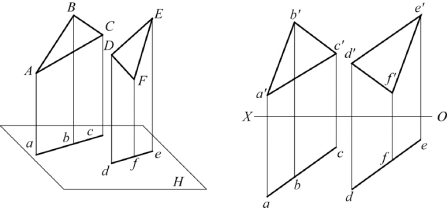
图2-58 两投影面垂直面相互平行
【例2-18】 已知投影如图2-59(a)所示,过点K作一平面与△ABC平行。
分析:由平面平行的几何条件,过点K作相交直线与△ABC上的两相交直线平行即可。
作图:过k′作k′m′∥a′b′,k′n′∥a′c′,过k作km∥ab和kn∥ac,如图2-59(b)所示。相交直线KM和K N所确定的平面即为所求。
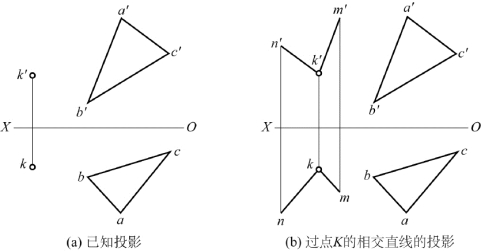
图2-59 作一平面和△ABC平行
2.相交问题
1)直线与平面相交
直线与平面相交,交点是直线与平面的共有点。下面介绍求交点投影的方法。
(1)一般位置直线与特殊位置平面相交。
一般位置直线与特殊位置平面相交,当特殊位置平面在某一投影面上的投影有积聚性时,交点的投影必在平面积聚性投影上,利用这一特性可以求出交点的投影,并判别可见性。判别可见性的方法有目测法和重影点法。
【例2-19】 已知投影如图2-60(a)所示,求作直线BC与铅垂面△EFG的交点K的投影,并判别可见性。
分析:因铅垂面△EFG的水平投影有积聚性,交点K的水平投影k为bc和fg的交点,再利用直线上点的投影特性求出k′,k′是b′c′可见段与不可见段的分界点。
作图:线段bc和fg的交点即为k,过点k作OX轴的垂线,交b′c′于k′,得点K的正面投影,如图2-60(b)所示。c′k′为可见段。
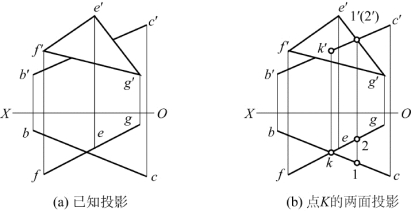
图2-60 求一般位置直线与铅垂面的交点
目测法判别可见性:假设平面是不透明的,交点K把线段BC分成两部分,有一部分被平面遮住看不见,由线段BC和铅垂面△EFG的水平投影可知,CK位于铅垂面△EFG右前方,因此c′k′可见,画成粗实线;b′k′在△e′f′g′内的部分不可见。
重影点法判别可见性:如图2-60(b)所示,正面投影中e′g′和c′k′的交点是线段BC上的点Ⅰ和铅垂面△EFG内EG边上点Ⅱ的重影。由水平投影可知1在2的前方,线段ⅠK可见,1′k′画粗实线,b′k′在△e′f′g′内的部分不可见。
(2)投影面垂直线与一般位置平面相交。
当直线是投影面垂直线时,可利用直线投影的积聚性求交点。
【例2-20】 已知投影如图2-61(a)所示,求作正垂线EF与△BCD的交点K的投影,并判别可见性。
分析:线段EF是正垂线,其正面投影具有积聚性,交点K是线段EF上的一个点,所以K点的正面投影k′和e′(f′)重合,因交点K也在△BCD上,故可利用平面上取点的方法,作出交点K的水平投影k。
作图:e′(f′)与k′重合,连接d′k′并延长,与b′c′交于m′;过m′作OX轴垂线,交bc于m,连接d、m,与ef交于k,k即为点K的水平投影,如图2-61(b)所示。
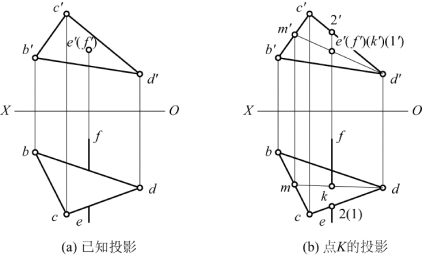
图2-61 求正垂线与一般位置平面的交点的投影
判别可见性:如图2-61(b)所示,线段EF和△BCD的三边都交叉,取其对水平投影面的重影点Ⅰ(在线段EF上)和点Ⅱ(在线段CD上)的水平投影,正面投影2′在1′的上方,则点Ⅱ的水平投影可见,点Ⅰ的不可见,线段EF上的ⅠK段位于△BCD下方,水平投影不可见,交点K另一侧线段KF位于△BCD上方,其水平投影可见,kf画粗实线。交点K的正面投影k′不可见。
2)平面与平面相交
平面与平面相交,交线是相交两平面的共有线,交线上的点都是相交两平面的共有点,因此,只要能够确定交线上的两个共有点,或者一个共有点和交线方向,即可作出两平面的交线。
(1)两特殊位置平面相交。
【例2-21】 已知投影如图2-62(a)所示,求作铅垂面△ABC与铅垂面△DEF的交线MN的投影,并判别可见性。
分析:因为两个平面都是铅垂面,所以交线为铅垂线,水平投影积聚为点,正面投影垂直于OX轴。
作图:如图2-62(b)所示,定出交线MN的水平投影m(n);过m(n)作OX轴垂线,与两个三角形的正面投影相交于m′、n′,就得到了交线MN的正面投影。
判别可见性:从水平投影看,在交线MN的左侧,△DEF在△ABC的前方,故△d′e′f′在m′n′左侧可见,而△a′b′c′在m′n′左侧的△d′e′f′范围内不可见;右侧则相反。
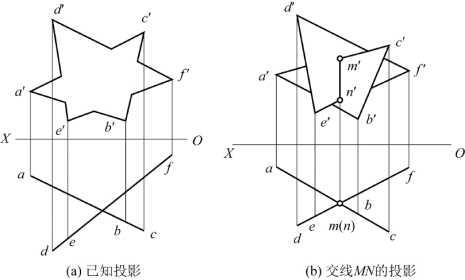
图2-62 求两铅垂面的交线的投影
(2)特殊位置平面与一般位置平面相交。
【例2-22】 已知投影如图2-63(a)所示,求铅垂面△DEF与一般位置平面△ABC的交线MN的投影,并判别可见性。
分析:由于铅垂面△DEF的水平投影有积聚性,交线MN的水平投影在其积聚性投影上,故交线的水平投影已知,利用直线上点的投影特性,可求出交线MN的正面投影。
作图:如图2-63(b)所示,依据铅垂面△DEF的积聚性投影,求出交线MN的水平投影mn。点m在ac上,点n在bc上,过m作OX轴垂线,交a′c′于m′;同理,求出交点N的正面投影n′。连接m′、n′,即得交线MN的正面投影。
重影点法判别可见性:如图2-63(b)所示,线段AB、EF上点Ⅰ、Ⅱ的正面投影重合,点Ⅰ在前,点Ⅱ在后,点Ⅰ在线段AB上,点Ⅱ在线段EF上,线段AB可见,则四边形a′b′n′m′可见,画粗实线,其他被遮住的部分不可见。同理,e′f′被四边形a′b′n′m′遮住的部分不可见,其他部分可见。
目测法判别可见性:如图2-63(b)所示,MN是可见与不可见的分界线。以水平投影mn为界,因四边形abnm在积聚性投影的前方,故△a′b′c′的正面投影中,a′b′n′m′可见,画粗实线,被△d′e′f′遮住的部分不可见。同理,△d′e′f′被a′b′n′m′遮住的部分不可见。
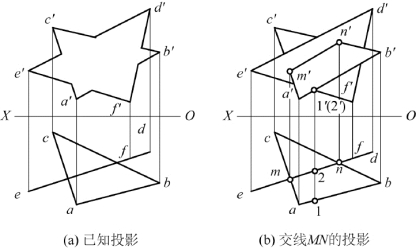
图2-63 求铅垂面与一般位置平面的交线的投影
![]()
假设光线能够透过物体,将物体各个顶点和各条棱线都在投影面上投射出影子,这些点和线的影子将组成一个能够反映物体形状的图形,这个图形通常称为物体的投影。投影的三要素是投影线、空间形体和投影面。投影法分为中心投影法和平行投影法两大类,平行投影法又分为正投影法和斜投影法。正投影法具有同素性、平行性、从属性、定比性、积聚性、实形性、类似性等特性。三面投影图的投影规律:长对正、高平齐、宽相等。
任何物体都可以看作点的集合。点是基本几何要素,研究点的投影规律是掌握其他几何要素投影规律的基础。
在三面投影体系中,依据直线与投影面的相对位置,可将直线分为三类,即投影面垂直线(铅垂线、正垂线、侧垂线)、投影面平行线(水平线、正平线、侧平线)和一般位置直线。空间两直线的相对位置有平行、相交、交叉三种。直角投影定理:空间两直线垂直相交,若其中一直线为某投影面平行线,则两直线在该投影面上的投影互相垂直。
根据平面在三面投影体系中的不同位置可将平面分为三类,即投影面垂直面(铅垂面、正垂面、侧垂面)、投影面平行面(水平面、正平面、侧平面)和一般位置平面。直线与平面及两平面的相对位置可分为平行、相交和垂直(垂直是相交的特例)。

一、选择题
1.在制图中,把光线称为( )。
A.投影中心 B.投影线 C.投影面 D.投影法
2.在制图中,把承受影子的面称为( )。
A.投影中心 B.投影线 C.投影面 D.投影法
3已知点A(20,0,0)和点B(20,0,10),关于点A和点B的相对位置,哪一种判断是正确的?( )。
A.点B在点A前面 B.点B在点A上方,且重影于V面上
C.点A在点B前面 D.点A在点B下方,且重影在OX轴上
4.在投影中心与投影面距离不变的情况下,形体距投影中心愈近,影子( )。
A.愈大 B.愈小 C.不变 D.无法确定
5.已知点A(0,10,25)和点B(0,15,25),关于点A和点B的相对位置,哪一种判断是正确的?( )。
A.点A在点B前面 B.点B在点A上方,且重影于V面上
C.点B在点A前面 D.点A在点B前面,且重影在OZ轴上
6.由一点放射投影线所产生的投影称为( )。
A.中心投影 B.水平投影 C.垂直投影 D.正投影
7.在三面投影图中,侧面投影图能反映形体的尺寸是( )。
A.长和高 B.长和宽 C.高和宽 D.长、宽和高
8.形成物体的基本几何元素包括( )。
A.点、直线和平面 B.点、曲线和曲面 C.点、曲线和平面 D.曲面、曲线、直线
9.点的正投影仍然是点,直线的正投影一般仍为直线(特殊情况除外),平面的正投影一般仍为原空间几何形状的平面(特殊情况除外),这种性质称为正投影的( )。
A.同素性 B.从属性 C.定比性 D.平行性
10.点在直线上,点的正投影一定在该直线的正投影上,点、直线在平面上,点和直线的正投影一定在该平面的正投影上,这种性质称为正投影的( )。
A.同素性 B.从属性 C.定比性 D.平行性
11.线段上的点将该线段分成的比例,等于点的正投影将线段的正投影所分成的比例,这种性质称为正投影的( )。
A.同素性 B.从属性 C.定比性 D.平行性
12.两直线平行,两直线上线段的长度之比等于线段正投影的长度之比,这种性质称为正投影的( )。
A.同素性 B.从属性 C.定比性 D.平行性
13.当线段或平面平行于投影面时,其线段的投影长度反映线段的实长,平面的投影与原平面图形全等,这种性质称为正投影的( )。
A.同素性 B.从属性 C.定比性 D.实形性
14.当直线或平面垂直于投影面时,直线的正投影积聚为一个点,平面的正投影积聚为一条直线。这种性质称为正投影的( )。
A.积聚性 B.从属性 C.定比性 D.实形性(https://www.xing528.com)
15.直线AB的V面投影反映实长,该直线为( )。
A.水平线 B.正平线 C.侧平线 D.侧垂线
二、填空题
1.工程上常采用的投影法是_________和平行投影法,其中平行投影法按投影线与投影面是否垂直又分为________和________。
2.当直线平行于投影面时,其投影_________,这种性质叫_________性;当直线垂直于投影面时,其投影________,这种性质叫________性;当平面倾斜于投影面时,其投影________,这种性质叫_________性。
3.主视图所在的投影面称为_________,用字母_________表示;俯视图所在的投影面称为________,用字母________表示;左视图所在的投影面称为________,用字母________表示。
4.三视图的投影规律是:主视图与俯视图_________;主视图与左视图_________;俯视图与左视图_________。
5.直线按其对三个投影面的相对位置关系的不同,可分为________、________和________。
6.与一个投影面垂直的直线,一定与其他两个投影面_________,这样的直线称为_________。
7.与一个投影面平行、与其他两个投影面倾斜的直线,称为_________,具体又可分为________、________和________。
8.空间平面按其对三个投影面的相对位置的不同,可分为_________、_________和_________。
三、判断题
1.当直线相对投影面倾斜时,直线的投影等于实长。( )
2.水平投影:从形体的上方向下方投影,在W面上得到的视图。( )
3.当直线垂直于投影面时,它在该投影面上的投影积聚为一点。( )
4.点的单面投影不能唯一确定点的空间位置。确定点的空间位置,至少需要两个投影面的投影。( )
5.点的投影仍然是点,直线的投影也可以是点。( )
6.中心投影法就是投影线互相平行的投影法。( )
7.当线段倾斜于投影面时,它在该投影面上的投影是缩短了的线段。( )
8.垂直于一个投影面的直线,必然平行于另外两个投影面。( )
四、简答题
1.正投影有哪些特性?
2.什么是重影点?如何解释其可见性?
3.试述直线投影规律。
4.试述直线投影的定比性。
五、工程制图与识图
1.已知点的两面投影如题图2-1所示,作出第三面投影。
2.已知A、B、C三点的各一投影a、b′、c″如题图2-2所示,且Bb′=10,Aa=20,Cc″=5。完成各点的三面投影,并用直线连接各面投影。
题图2-1
题图2-2
3.已知点A(22,8,5)、B(6,15,18),单位为mm,在题图2-3中求作点A和点B的三面投影,并比较两点的空间位置。
点A在点B之_________(前、后)_________mm;
点A在点B之________(左、右)________mm;
点A在点B之_________(上、下)_________mm。
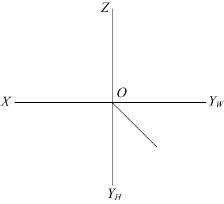
题图2-3
4.如题图2-4所示,求下列直线的第三面投影,并判别各直线与投影面的相对位置。
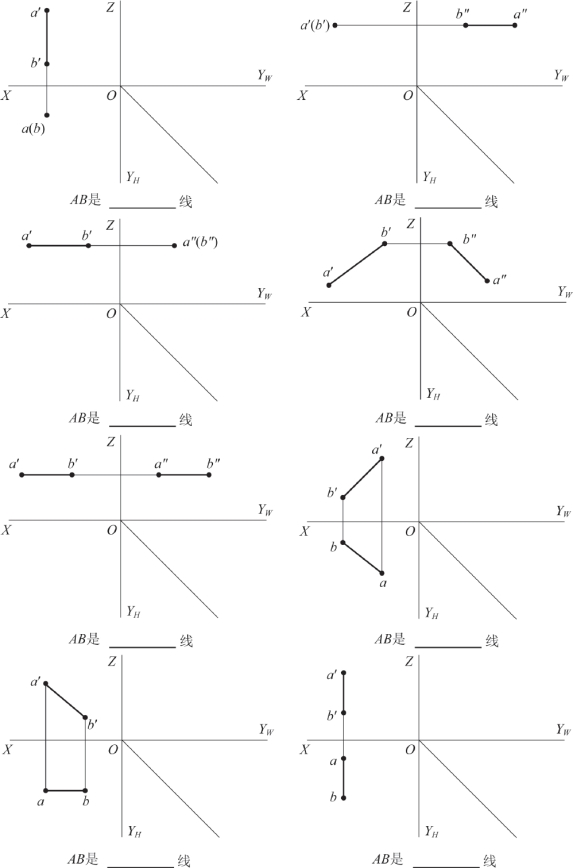
题图2-4
5.已知水平线AB与铅垂线MN相交于点M,投影如题图2-5所示,试完成两直线的三面投影图。
6.如题图2-6所示,作图判别点K是否在直线AB上。
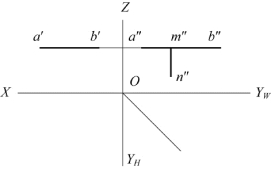
题图2-5
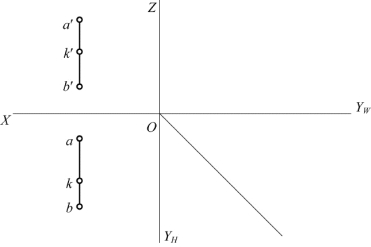
题图2-6
7.如题图2-7所示,在直线AB上取一点C,使AC∶CB=4∶3。作出C点的两面投影。
8.如题图2-8所示,已知AB∥W面,AB=20 mm,α=30°,点B在A的后上方,求作AB的三面投影。
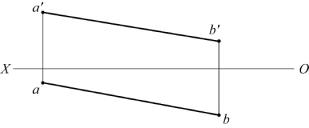
题图2-7
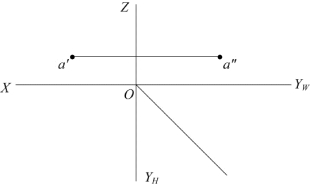
题图2-8
9.如题图2-9所示,作图求AB的实长和它与水平面的倾角α。
10.如题图2-10所示,作图求AB的实长和它与正面投影面的倾角β。
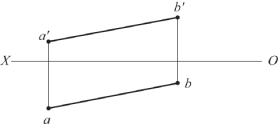
题图2-9
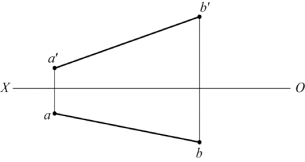
题图2-10
11.已知a′b′及b(见题图2-11),β=30°,且A在B之前,作图求AB的实长及ab。
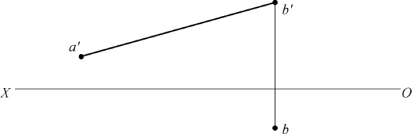
题图2-11
12.如题图2-12所示,作直线GH,使其与EF和CD相交且与AB平行。
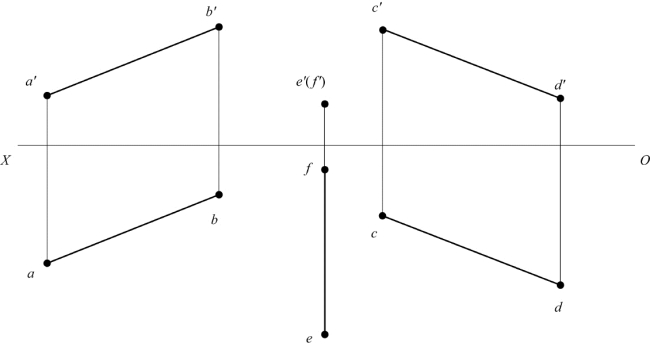
题图2-12
13.判别题图2-13中两直线的相对位置。
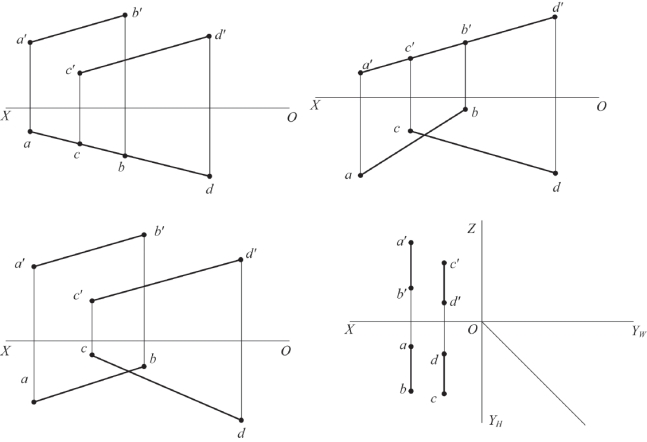
题图2-13
14.如题图2-14所示,过点K作一直线与AB和CD都相交。
15.如题图2-15所示,判别交叉直线重影点的可见性。
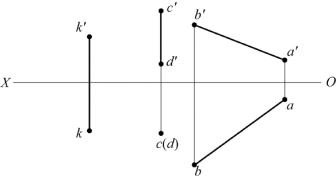
题图2-14
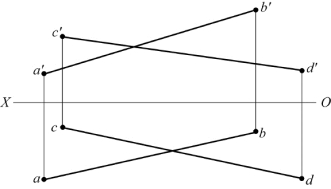
题图2-15
16.已知AB的H、V面投影和K点的V面投影,如题图2-16所示,过K点作水平线KL与AB垂直相交,L为垂足。求作KL的两面投影。
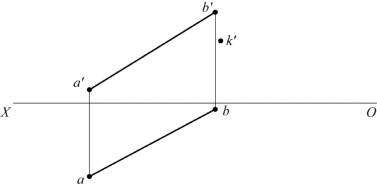
题图2-16
17.如题图2-17所示,求点M到水平线AB的距离。
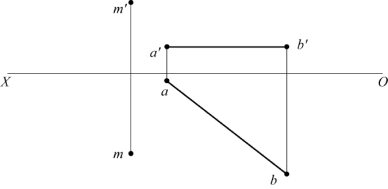
题图2-17
18.如题图2-18所示,求点N到正平线AB的距离。
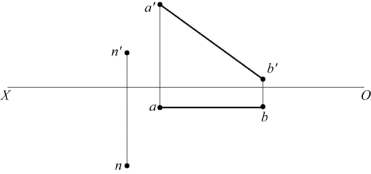
题图2-18
19.如题图2-19所示,求直线AB与CD的距离。
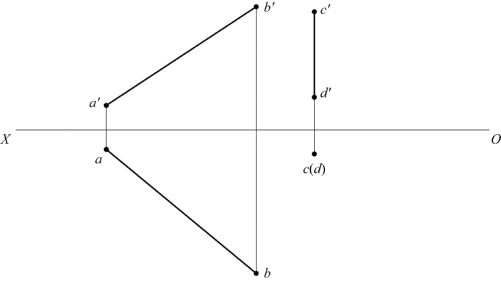
题图2-19
20.如题图2-20所示,已知△ABC等腰三角形,C点在直线DE上,AB∥V面,求作△ABC的两面投影。
21.如题图2-21所示,已知AB∥V面,AB垂直于BC,BC=30 mm,C点在V面上,C在B之下,求BC的两面投影。
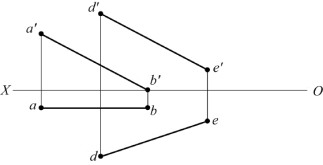
题图2-20
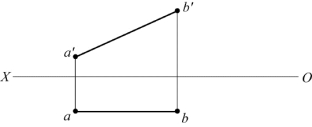
题图2-21
22.如题图2-22所示,求平面内点的另一个投影。
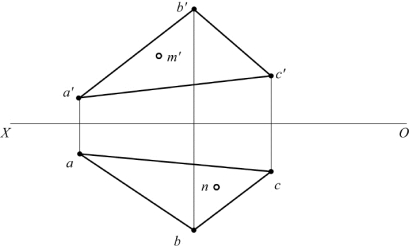
题图2-22
23.补画出题图2-23中平面的第三个投影,并判断平面与投影面的相对位置。
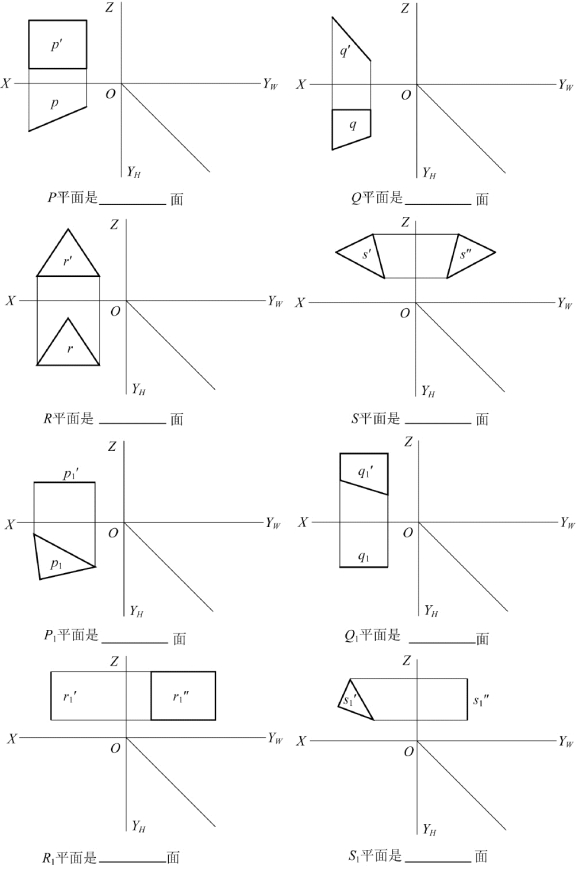
题图2-23
24.如题图2-24所示,求三角形ABC所在平面内的直线EF的H面投影。
25.如题图2-25所示,求平面ABCD内字母“A”的另一面投影。
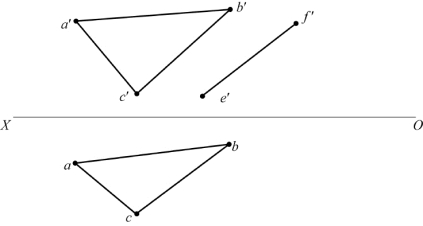
题图2-24
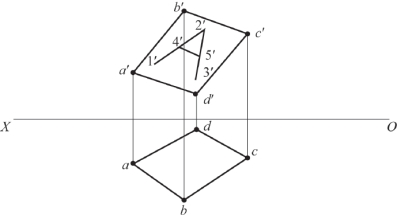
题图2-25
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




