无人驾驶车辆模型预测控制探究

考虑横摆、侧滑和侧倾等操控稳定性相关动力学约束的无人驾驶车辆轨迹跟踪控制问题可以被转换为二次型最优求解问题，并通过实时求解生成能够有效避险且满足操纵稳定性要求的最优控制序列。性能评价函数如式(8.6)所示。

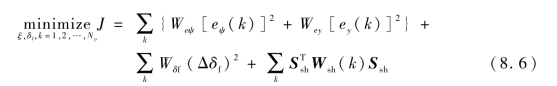
其中，等号右边第一项抑制了无人驾驶车辆相对于参考路径的横向偏差和航向偏差，体现了跟踪给定参考轨迹的期望；第二项限制了控制输入的变化量，使最优控制输入尽量平滑；第三项对车辆横摆稳定性约束的松弛因子进行了惩罚，从而促使无人驾驶车辆的状态尽量在横摆稳定性判据给出的约束之内。

另外，在优化求解过程中还考虑了车辆的动力学模型约束、基于包络线的横摆稳定性约束、基于零力矩点的侧倾稳定性约束、道路环境约束以及车辆执行机构和底层驱动能力的约束等。因此，综合考虑无人驾驶车辆操作稳定性要求和安全行驶约束的基于模型预测的轨迹跟踪控制问题可以写作

式(8.7)中待优化的变量是车辆前轮偏角控制量(δf)，以及滑移约束的松弛因子Ssh。松弛因子的存在是为了通过允许高速车辆出现暂时性滑移现象来保证此优化问题始终可以找到可行解。需要调试的参数为Wδf、Wey、Weψ和松弛因子的权重Wsh。通过选取不同的权重可以体现出优化目标的优先级。通过对车辆滑移约束施加一定的松弛因子，可以保证当道路的无碰撞轨迹与稳定性约束发生冲突时，优先保证车辆在可行区域内行驶，即允许车辆暂时发生滑移。

在理想状态下，无人驾驶车辆进行轨迹跟踪控制时，式(8.7)中的约束都能够被满足。然而，在紧急情况下或者是复杂道路环境中，这些安全行驶的约束可能会彼此冲突，因此需要对约束条件设置不同的优先级，系统的权衡轨迹跟踪时优先达成的目标，可以通过设定权重系数的相对大小来实现。通过设定Wαsh，Wψsh＞＞Weψ，Wey＞＞Wδf，一方面能够抑制车辆进入动力学非稳定区域；另一方面可以保证当道路的无碰撞轨迹与横摆稳定性约束发生冲突时，优先保证车辆在可行区域内行驶，即允许轮胎暂时进入非线性区域，以达到防止车辆发生碰撞的目的。(www.xing528.com)

代价函数中式8.7(a)抑制了高速无人驾驶车辆相对于参考路径的横向偏差和航向偏差，体现了路径跟踪的期望；式8.7(b)建立了跟踪参考路径与控制量平滑之间的关系；式8.7(c)对车辆滑移稳定性约束的松弛因子进行惩罚，从而促使高速车辆尽量不出现滑移现象；式8.7(d)和式8.7(e)分别为变步长离散方法得到的车辆动力学等效模型；式8.7(f)～式8.7(h)分别为针对高速车辆行驶过程中稳定性的包络线滑移约束、零力矩点侧倾约束和道路环境约束；式8.7(i)和式8.7(j)体现了车辆执行机构和底层驱动能力的约束。

由于式(8.7)的性能评价函数中不同评价指标的单位不同，而且在车辆模型离散时选择了变步长的模型离散化方法，所以增加了权重系数调节的难度。为了更好地进行参数调整，需要对跟踪偏差及横摆稳定性约束的松弛量相对于其阈值进行归一化处理，并按照不同的离散化步长，对权重因子按适当的比例进行缩放：

利用第3章和第4章描述的方法，可将MPC控制问题转化为二次型规划问题，然后调用成熟的求解器进行求解，优化得到前轮偏角的最优控制序列。模型预测控制使用的参数数值说明如表8.1所示。

表8.1　模型预测控制使用的参数数值说明