无人车模型的5次多项式轨迹拟合

在轨迹重规划算法中，将目标函数设定为有限时域内与参考点的距离偏差最小，所规划出的轨迹是以预测时域内离散的点给出的。随着预测时域的增加，这些局部参考轨迹点的数量也会随之增加。直接将这些点输入控制层，占用了过多的控制器输入接口，不利于控制器的规范化设计。另外，由于规划层与控制层的控制周期并不一致，控制层很难根据离散的参考轨迹点完成轨迹跟踪的任务。

综合上述因素，有必要对轨迹重规划算法所规划出的局部参考路径进行处理，实现规划层与控制层的顺利对接。曲线拟合是对离散点处理的主要方式，根据所采用曲线的不同，有样条曲线拟合、多项式拟合以及幂指数拟合等。由于车辆存在运动学约束，如车辆位置连续要求曲线是连续的，横摆角连续要求曲线是一阶连续的，而加速度约束则要求曲线二阶连续。因此，本书选择5次多项式作为拟合曲线，形式如下：

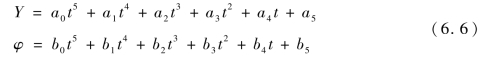
其中，ap=[a0，a1，a2，a3，a4，a5]，bp=[b0，b1，b2，b3，b4，b5]为待求参数。

设规划层预测时域Np=16，拟合结果如图6.6所示。图6.6中，星号为轨迹重规划算法在预测时域内规划出的离散点，曲线为拟合后的轨迹曲线。

以拟合后各数据点残差的范数来表征拟合质量，对整个轨迹重规划过程中的201次规划数据进行统计，统计结果如图6.7所示。从图中可以看出，车辆位置横坐标Y的拟合残差最大值为0.003，车体航向角φ的拟合残差最大值不超过7.50×10-5，具备非常高的拟合精度。

图6.6　离散轨迹点拟合结果(www.xing528.com)

(a)横向位置拟合结果；(b)横摆角拟合结果

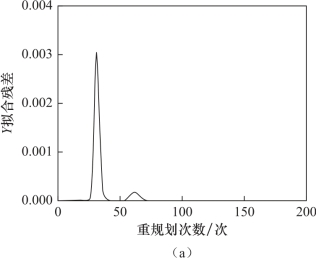
图6.7　数据点拟合质量统计

(a)横向位置Y的拟合残差

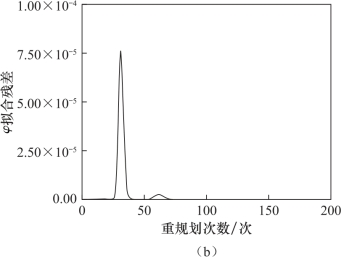
图6.7　数据点拟合质量统计(续)

(b)横摆角