基于递推最小二乘法的轮胎侧偏刚度估计

基于车辆动力学模型进行模型预测控制需要用到车辆的状态信息、惯性参数、参考道路信息以及轮胎线性侧偏刚度等。其中，车辆的状态信息包括纵向速度(vx)、侧向速度(vy)和前轮偏角(δf)等，车辆惯性参数包括车身质量(m)、车体转动惯量(Ix、Iz)和质心到前后轴的距离位置(lf、lr)等，参考道路信息包括路面倾角(φt)和道路参考曲率(κref)等。鉴于车辆的状态信息、惯性参数以及参考道路信息可以在仿真环境中直接获得，而且现有文献对于实时的车辆状态估计和车辆惯性参数在线识别已有了系统的研究，并取得了较好的应用效果，这里不再赘述。本小节重点关注前、后轴线性侧偏刚度的估计。

轮胎线性侧偏刚度是对车辆模型进行线性化的重要参数，反映了车辆在轮胎线性区域内的操纵稳定特性，而且随着行驶工况、路面条件的不同，此参数往往发生变化。因对此轮胎线性侧偏刚度进行实时估计可以提高无人驾驶车辆对不同附着系数路面的适应性，下面根据车辆的状态信息和惯性参数的历史数据，采用递归最小二乘法估计轮胎的线性侧偏刚度。

假设所研究的历史数据窗口长度为N，采用缓冲数列方法将N组数据绑定为一个数组，根据式(2.23)和式(2.24)可以得到轮胎侧偏力与轮胎线性侧偏刚度的线性回归方程：

式(5.16)选择使用轮胎侧向力和轮胎侧偏角来估计轮胎的线性侧偏刚度，这是因为在仿真环境下这两个参数容易获得。然而，现实中对轮胎侧向力及其侧偏角难以直接测量或者测量成本较高，限制了本方法的应用。因此，在实际应用中应该结合车载传感器的配置，选择合适的车辆状态参数来建立线性回归方程。

基于递推最小二乘法的模型参数估计原理可以表述为：在所研究的历史数据窗口内，使实际值与估计值的平方差最小，其代价函数J可表示为

其中，λm为遗忘因子，N为时间窗口的长度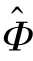，(k)表示模型参数的估计值。

要使式(5.17)取最小值，应满足代价函数J对未知参数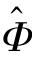的偏导数等于0，即

由式(5.18)可得

令(www.xing528.com)

式(5.20)可表示为

由式(5.21)可得

将式(5.24)分别乘以P(k)和P(k-1)，可得

设K(k)=P(k)φ(k)为递推增益，则式(5.25)可以改写为

将式(5.22)和式(5.26)代入式(5.23)可得

由式(5.26)可以得到递推增益K(k)的递推公式：

式(5.26)～式(5.28)即为递推最小二乘法的递推公式。