5种仿真工况下无人驾驶车辆模型的预测控制结果

所设计的主动转向跟踪控制器以车辆前轮偏角作为控制器的输入，控制目标是通过不断减少与参考轨迹的偏差，跟踪参考轨迹。为了更加全面地分析所提出控制方法的可行性，本书设计三种不同的仿真工况，尽可能体现控制器在实际运用时可能遇到的各种情况。

1.控制系统对路面附着条件的鲁棒性

无人驾驶车辆在不同附着条件的道路上(如干燥路面、湿滑路面)行驶时，车辆自身的动力学参数，如轮胎侧偏刚度等将会发生变化，同时也会出现地面提供的侧向力不足的情况。这给控制器的性能带来了一定的挑战。仿真工况1就是在不同附着条件的道路上对车辆轨迹跟踪能力进行测试。无人驾驶车辆正常行驶路面的附着系数为μ=0.7～1，湿滑路面的附着系数为μ=0.4左右。因此，分别选取μ为0.4和0.8两种情况进行测试。

车辆纵向速度设定为30 m/s，轨迹跟踪控制器的基本参数设定为：T=0.05 s，Np=25，Nc=15，-10°≤δf≤10°，-0.85°≤Δδf≤0.85°，权重矩阵设置为

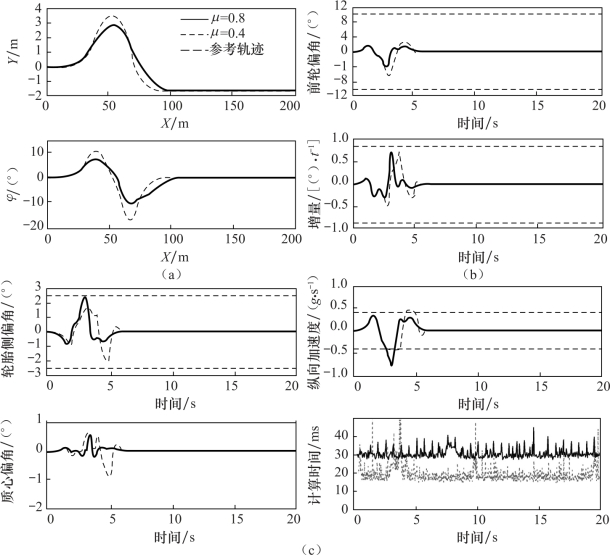
图5.7　仿真工况1的仿真结果

(a)输出量随时间变化的历程；(b)控制量随时间变化的历程；(c)约束量随时间变化的历程

　　仿真结果如图5.7所示。其中，图5.7(a)所示为系统输出量[Y，φ]随时间变化的关系，图5.7(b)所示为系统控制量δf和控制增量Δδf随时间变化的关系，图5.7(c)所示为所设定的动力学约束条件在仿真过程中的变化。从图5.7(a)中的曲线可以看出，控制器在不同附着条件的路面上都能很好地跟踪期望轨迹，但附着条件良好时车辆的跟踪误差能够进一步缩小。若附着条件较差，地面不能提供足够的侧向力，车辆转向时横摆角会出现较大偏差[图5.7(a)中70 m处]，轨迹跟踪控制器能够及时修正偏差，最终将偏差收敛为0。从图5.7(b)中可以看出，跟踪过程中车辆的控制量以及控制增量都处于约束范围内，保证了给定车辆的控制量能被执行机构顺利执行。图5.7(c)中，除了设定为软约束的纵向加速度外，各项约束都被限定在了给定的区间范围内。软约束的加入保证系统能够在给定时间内得到可行解。综合上述分析，控制系统能够在不同附着条件下较好地跟踪期望轨迹，且具备良好的稳定性。

2.控制算法对速度的鲁棒性

很多控制算法往往需要针对不同的行驶速度确定不同的控制参数，而模型预测控制器能够根据建立的车辆模型预测系统未来的输出，对车速的变化具有很强的鲁棒性。仿真工况2就是在不同的车速下，以相同参数的控制器实现对无人驾驶车辆的主动转向控制，分析控制器对不同车速的鲁棒性。

主动转向仿真实验分别在10 m/s、20 m/s和30 m/s的速度下进行，道路附着条件良好，μ=0.8。控制器所采用的参数为：T=0.05 s，Np=25，Nc=10，-10°≤δf≤10°，-0.85°≤Δδf≤0.85°，权重矩阵设置为

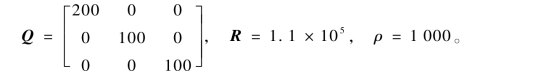(www.xing528.com)

　　仿真工况2的仿真结果如图5.8所示。其中，图5.8(a)所示为三种不同车速下车辆的轨迹跟踪对比，图5.8(b)所示为控制量和控制增量随时间变化的曲线，图5.8(c)所示为动力学约束随时间变化的曲线，实线、点线和点画线分别对应车速为10 m/s、20 m/s和30 m/s的仿真结果。从图5.8(a)可以看出，在相同控制参数下，不同速度行驶的车辆都具备良好的轨迹跟踪性能，体现出对速度很强的鲁棒性。在图5.8(b)中，不同速度下控制量的增量差异较大，速度越高，控制量增量就越大，但始终保持在约束范围内。图5.8(c)中各动力学约束保持在给定的区间范围内，质心侧偏角则远低于极限范围，表明车辆行驶过程非常平稳。因此，本书所设计的轨迹跟踪控制器能够在不同车速下完成对期望轨迹的跟踪，车速增加并不会导致车辆稳定性能的下降。

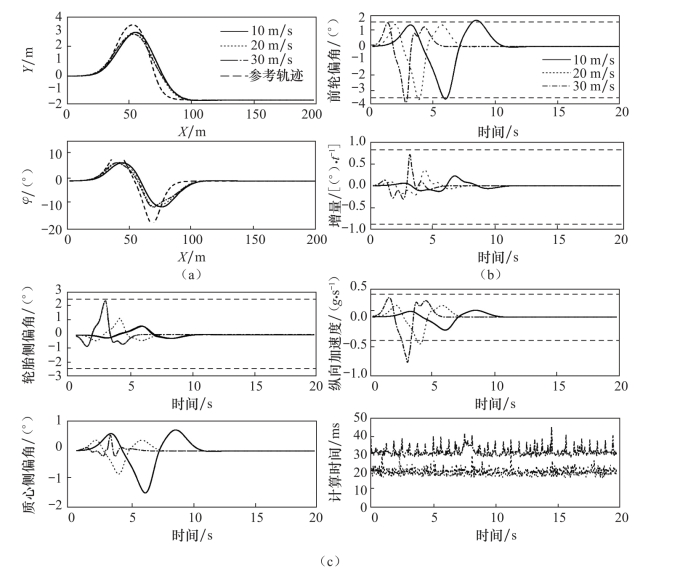
图5.8　仿真工况2的仿真结果

(a)输出量随时间变化的历程；(b)控制量随时间变化的历程；(c)约束量随时间变化的历程

3.不同设计参数对控制器的影响

不同参数对控制器性能的影响有所差异。对于模型控制算法来说，最重要的设计参数就是预测时域与控制时域。为了考察不同时域对控制器跟踪性能和计算量的影响，分别设计了控制器A和控制器B。控制器A所采用的参数如下：T=0.05 s，Np=25，Nc=10，-10°≤δf≤10°，-0.85°≤Δδf≤0.85°，μ=0.8，权重矩阵设置为

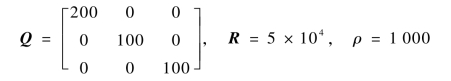
　　相比控制器A，控制器B减少了预测时域和控制时域的步长，设定Np=15，Nc=1，其余参数与控制器A保持一致。分别在不同的控制器作用下，验证无人驾驶车辆轨迹跟踪及保持稳定行驶的能力。

仿真工况3的仿真结果如图5.9所示。其中，图5.9(a)所示为两个控制跟踪期望轨迹的对比，图5.9(b)所示为两个控制器在每个周期内的计算时间，图中实线和点线分别对应控制器A、B的仿真结果。从图5.9(a)可以看出，控制器B能够跟踪期望轨迹，并且最终能够将偏差收敛为0。与控制器A的跟踪效果相比，控制器B的跟踪偏差较大，尤其是对期望横摆角的跟踪；但控制器B并不是一无是处，图5.9(b)中的曲线可以非常直观地显示出，控制器B的计算时间要远低于控制器A，平均只有不到10 ms。因此，采用较小的预测时域和控制时域对于提升控制系统的实时性效果明显。在硬件条件较低而又期望保证系统的实时性情况下，可以采用这样的设计方法。

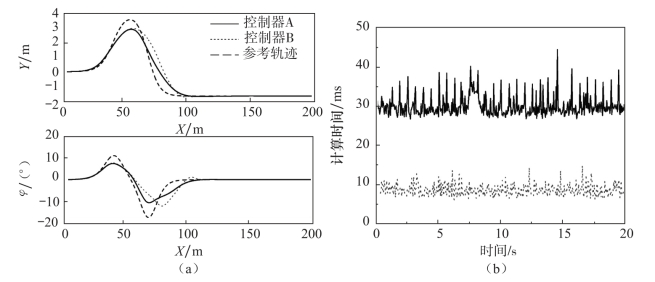
图5.9　仿真工况3的仿真结果

(a)输出量随时间变化的关系；(b)不同控制器的计算时间