本书主要考虑控制过程中的控制量极限约束和控制增量约束，控制量表达形式为
控制增量约束表达形式为
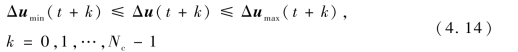
在目标函数中，求解的变量为控制时域内的控制增量，约束条件中也只能以控制增量或者控制增量与转换矩阵相乘的形式出现。因此，需要对式(4.14)进行转换，求得相应的转换矩阵。因为存在如下关系：
设：
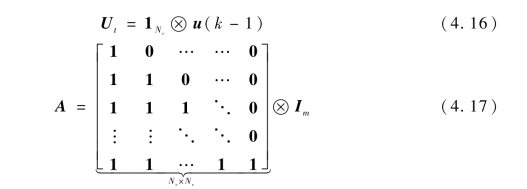
其中，1Nc为行数为Nc的列向量；Im为维度为m的单位矩阵；⊗为克罗内克积(Kronecker product)；u(k-1)为上一时刻实际的控制量。
结合式(4.15)～式(4.17)，可以将式(4.13)转换为以下形式：
其中，Umin，Umax分别为控制时域内的控制量最小值、最大值集合。
将目标函数转化为标准二次型形式并结合约束条件，解决以下优化问题：
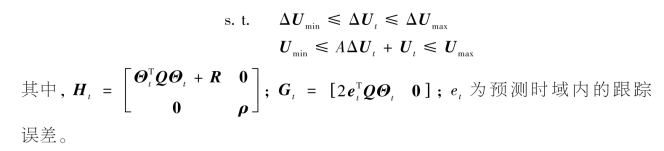
在每一控制周期内完成对式(4.19)的求解后，得到控制时域内的一系列控制输入增量：
(www.xing528.com)
将该控制序列中第一个元素作为实际的控制输入增量作用于系统，即
进入下一个控制周期后，重复上述过程，如此循环实现了对车辆的轨迹跟踪控制。
约束条件中涉及的具体数值则需要通过下面介绍的纵横向跟踪能力测试获得。
在无人驾驶车辆纵向跟踪能力实验中，分别对无人驾驶车辆输入5 m/s、7.5 m/s和10 m/s的阶跃期望速度，平稳行驶一段时间后再以最大制动能力对车辆进行制动，记录加速和减速时间，测试结果如表4.1所示。可以看出，车辆在中低速(7.5 m/s以下)加减速过程中较为平稳，加速度维持在1 m/s2左右。为了使跟踪过程更加平稳，无人驾驶车辆速度控制约束可设置为
其中，vd为车辆期望速度，Δv为每个控制周期的速度增量。
表4.1 无人驾驶车辆纵向跟踪能力测试
在横向跟踪能力实验中，将车辆前轮从左极限位置连续转向至右极限位置，记录相应的位置和时间，测试结果如表4.2所示。通过计算可知，转向盘转一圈大约需要1.8 s，对应于前轮偏角为17°。因此将车辆极限前轮偏角和前轮偏角增量设置为
表4.2 无人驾驶车辆原地转向性能测试
结合式(4.22)和式(4.23)，可以得到控制量的约束条件为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
