基于MPC工具箱的速度控制实例

通过3.1节中的理论介绍，相信大家对模型预测控制的三项基本原理有了一定的认识。下面我们通过在MATLAB中实现一个简单的速度跟踪控制实例来分析模型预测控制在实际应用时的基本思路。

车辆的纵向控制可以被简化为一个双积分系统，表示为

其中，v和a分别为车辆的速度和加速度，j表示车辆加速度的变化率，为控制输入。

下面我们通过MATLAB中的模型预测控制工具箱(Model Predictive Control Toolbox)来实现这一仿真。MATLAB的MPC工具箱是集成在MATLAB环境下的工具包之一，提供了一系列用于模型预测控制的分析、设计和仿真的函数。这个工具箱使用简单，能够帮助初学者顺利上手。同时，工具箱中提供了一系列实际控制例程作为教学使用。我们在开始学习模型预测控制时，就可以从这些案例出发。

在Windows中运行MATLAB主程序，并在控制命令窗口输入“demo”命令，打开MATLAB的例程教学窗口。在搜索框中输入“Model Predictive Control Toolbox Examples”，即可找到该工具箱所提供的例程，如图3.3所示。考虑到式(3.1)是一个单输入单输出系统，我们选择“Control of a Single→Input→Single→Output Plant”这一例程。

单击例 程 中 的 第 一 个 项 目“Control of a Single→Input→Single→Output Plant”，我们可以在右侧窗口看到这个例程的介绍、源代码以及结果展示。单击窗口右上角的“Open this Example”，程序会自动打开相应的M文件，如图3.4中黑色矩形框所示。单击运行按钮或者键盘F5，可以运行此程序，查看运行结果。

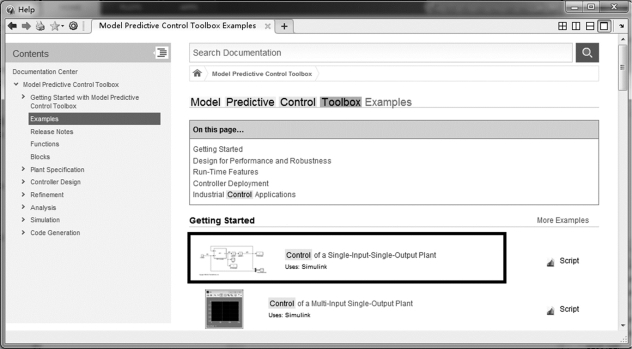
图3.3　MATLAB例程教学窗口的MPC工具箱界面

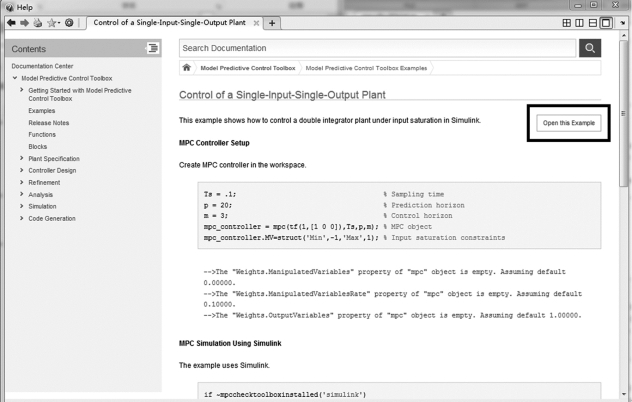
图3.4　MATLAB例程界面

　　运行结果包含三个窗口，如图3.5所示。其中，左侧窗口为Simulink环境下搭建的控制系统，右侧两个窗口分别为被控系统的输入和输出。从被控系统输出可以看出，该系统的控制目标是跟踪一条固定轨迹。系统状态从0出发，在控制器的作用下，逐渐跟踪上了期望轨迹。从被控系统输入可以看出，输入值被成功限定在-1～1。

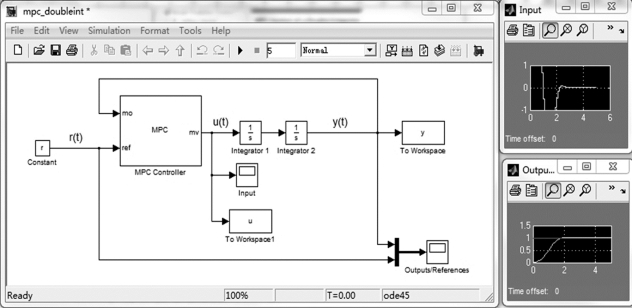
图3.5　运行结果(www.xing528.com)

那么，这个控制系统是如何实现功能的呢?通过分析控制系统发现，整个控制器主要由两部分组成：模型预测控制器和被控系统(双积分系统)，如图3.6所示。具体的输入输出关系如下：模型预测控制器的输入为参考轨迹和系统状态，输出为MPC优化得到的控制量，被控系统的输入为控制器输出的控制量，然后将自身的状态量反馈到MPC控制器中。明确输入输出关系能够为后续自行设计控制系统奠定基础。

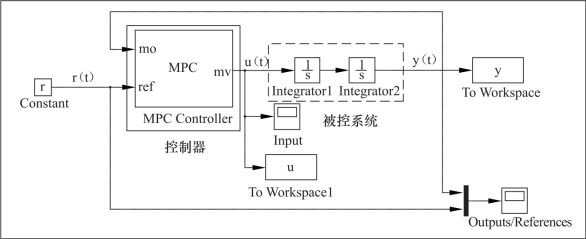
图3.6　控制系统分析

在对整个控制系统有了基本概念后，我们将目光转到代码层面，探究一个标准的模型预测控制器究竟如何工作。在之前所打开的“mpcdoubleint.m”文件中，首先是对程序的说明以及版权的申明，然后按照不同的步骤分块进行程序编写。今后我们在编写自己的控制算法时，也可以参考这样的写法。在程序主体内容中，我们将重点放在模型预测控制器的设置上面，也就是如下一段代码：

这段代码中完成了构建模型预测控制器必要的设置。首先是对系统采样时间的设置，然后确定了预测时域和控制时域(这两者的区别将在之后的章节中介绍)，紧接着是通过调用系统函数tf()以传递函数的形式实现系统建模，最后通过调用模型预测工具箱函数mpc()完成控制器的设定。为了实现对控制输入的限制，代码还加入了控制量的上下界约束条件。

一般来说，模型预测控制器需要给定被控系统的采样时间、预测时域、控制时域和预测模型。如果需要加入系统的约束，还需要进一步给定约束条件。读者在编写控制算法的时候，也建议将这些参数作为基本的传递参数，这样不仅能保证设置准确可靠，还能提高代码可读性。

由于是在Simulink环境下的仿真，还需要对仿真环境进行设置，包括系统初始状态、仿真时间和参考轨迹，代码如下：

其中，x01表示车辆的加速度，x02表示车辆的速度，MPC控制器的输出为加速度的变化率j。运行仿真程序，MPC控制器的输出经过双积分系统后得到车辆的速度又被反馈给MPC控制器，如此往复循环，就完成了整个控制系统。

我们分析了整个程序之后，会发现这个例子其实非常简单。通过简单的参数设置和环境设置，就可以完成一个双积分系统对固定轨迹的跟踪，并且对输入输出进行了约束限制。为了加深对程序的理解，我们可以自己尝试修改相关参数，如预测时域、采样时间等，观看不同参数的控制效果。在对模型预测控制有了一定的认识后，可以分别修改控制器与被控对象，搭建自己的仿真平台。

介绍完模型预测控制工具箱中的例程，相信大家对模型预测控制如何使用已经有了一个直观的认识。但在刚才的分析中，我们只学习了如何去设置模型预测控制器的参数，没有涉及模型预测控制器的内部结构，而且MPC工具箱只能用于较简单的场景，难以适应更加复杂的模型和环境。下面介绍适用于更复杂环境，且更符合实际情况的速度跟踪控制方法，并讲解模型预测控制问题转换为计算机程序应用的方法。