【摘要】：道路倾角与曲率对无人驾驶车辆的操纵稳定性有着重要影响，直接关系到车辆动力学模型的准确程度。结合上一小节得到的综合考虑横摆、侧滑和侧倾约束的车辆动力学模型，建立考虑道路倾角及曲率影响的车辆动力学模型，如图2.12所示。图2.12考虑侧倾约束的车辆动力学模型跟踪时变曲率道路示意考虑侧倾约束的车辆动力学模型跟踪时变曲率参考道路的跟踪误差方程可由式得到，即=-κrefvx=vxeφ+vy。
道路倾角与曲率对无人驾驶车辆的操纵稳定性有着重要影响，直接关系到车辆动力学模型的准确程度。结合上一小节得到的综合考虑横摆、侧滑和侧倾约束的车辆动力学模型，建立考虑道路倾角及曲率影响的车辆动力学模型，如图2.12所示。
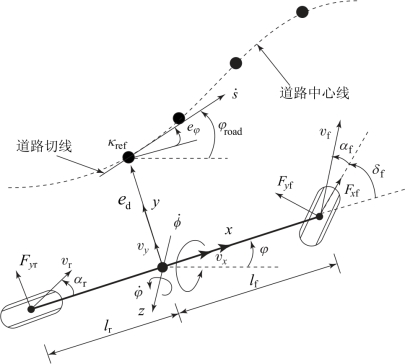
图2.12 考虑侧倾约束的车辆动力学模型跟踪时变曲率道路示意
考虑侧倾约束的车辆动力学模型跟踪时变曲率参考道路的跟踪误差方程可由式 (2.12)得到，即
=
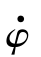-κrefvx
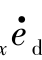=vxeφ+vy。
考虑存在道路倾角φt的情况(图2.13)，车辆质心处受到的合力在y轴上的分力可表示为
图2.13 考虑道路倾角与曲率的车辆动力学模型示意(www.xing528.com)
由于车辆悬架系统变形产生的车体侧倾角为φr=φ-φt，其变化率为
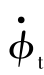，假设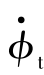
≈0，则车辆悬架系统所产生的侧倾阻力矩Mx可以表示为
通过对式(2.49)进行变形，可以得到考虑道路倾角与曲率的综合等效约束车辆动力学模型：
鉴于车辆动力学模型的推导涉及复杂的矩阵运算和多个参数变量，为方便读者对不同的车辆动力学模型进行线性化处理，以下提供本书在处理过程中所用的MATLAB代码，MATLAB程序为“chapter_2_3_2.m”。读者根据自定义的车辆动力学模型修改程序中对应的微分方程就可以得到最终结果。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
