无人车横摆动力学模型：考虑道路曲率

车辆横摆动力学模型是无人驾驶车辆路径跟踪控制中常用的模型之一。但是式(2.17)所表示的车辆横摆动力学模型对于模型预测控制器的设计来说还是过于复杂，因此需要对其进行进一步简化。首先，对前轮偏角δf做小角度假设，即cos(δf)≈1，sin(δf)≈δf，则式(2.17)可以写作

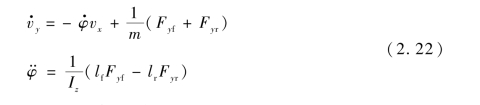
此时，式(2.22)所表示的车辆动力学模型的非线性特征主要来自轮胎非线性区的轮胎力表达，可以使用上一节推导的线性化轮胎模型对轮胎侧向力进行线性化：

由于线性化轮胎模型只在轮胎侧偏角较小时具有较高的拟合精度，所以采用小角度假设可近似得到

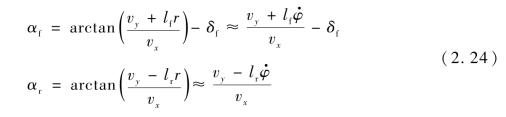
对于单轨车辆模型，可以忽略轮胎的横向载荷转移，其轮胎垂向载荷可以表示为

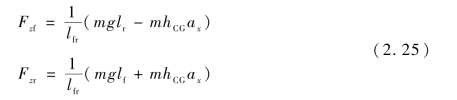
其中，hCG为车辆质心高度，ax为纵向加速度。

结合式(2.22)～式(2.25)，可以得到基于前轮偏角小角度假设和线性化轮胎模型的车辆横摆动力学模型。令ξ=[vy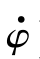]T为状态矢量，u1=δf为输入矢量，线性化的车辆横摆动力学模型可以写成状态空间方程的形式：(www.xing528.com)

式(2.26)所表示的车辆横摆动力学模型能够反映车辆的横摆特性，常被用于车辆的横摆稳定性分析。然而，此模型的不足在于没有考虑车辆的侧倾动力学特性，无法体现车辆的侧倾稳定性约束，不适用于存在复杂道路倾角的路径跟踪控制。

当无人驾驶车辆进行路径跟踪时，道路曲率对其转向特性和行驶稳定性也有重要影响，直接关系到无人驾驶车辆动力学模型的准确程度。因此，当车辆横摆动力学应用于无人驾驶车辆的路径跟踪控制时，还需要考虑道路曲率的影响，如图2.9所示。

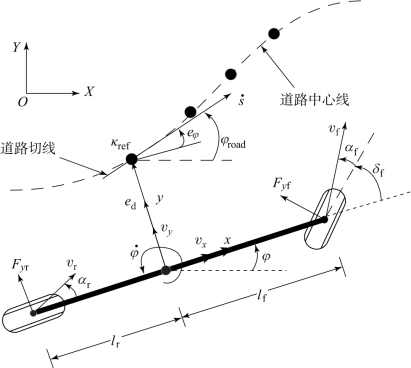
图2.9　考虑路径跟踪的车辆横摆动力学模型示意

将式(2.5)、式(2.12)与式(2.22)相结合，得到考虑道路曲率的车辆横摆动力学模型：

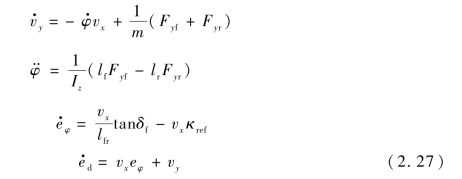
其中，κref为由期望路径得到的参考曲率。