【摘要】：在后轴行驶轴心处，速度为前、后轴的运动学约束为由式(2.1)和式(2.2)联合可得根据前后轮的几何关系可得将式(2.3)和式(2.4)代入式(2.2)，可解得横摆角速度为其中，ω为车辆横摆角速度；同时，由ω和车速vr可得到转向半径R和前轮偏角δf：由式(2.3)和式(2.5)可得到车辆运动学模型为该模型可被进一步表示为更为一般的形式：其中，状态量ξkin=[Xr，Yr，φ]T，控制量ukin=[vr，δf]T。
图2.1 车辆运动模型
描述车辆的运动通常涉及两个坐标系：惯性坐标系XOY和车体坐标系xoy，如图2.1所示。其中，惯性坐标系为惯性导航系统使用的坐标系，而车体坐标系主要用于描述车辆的相对运动。本书中定义惯性坐标系的X轴指向东向，Y轴指向北向，Z轴向上为正；定义车体坐标系x轴为车辆前方，y轴指向车辆左侧。此时，车辆的横摆角φ定义为车体坐标系x轴与惯性坐标系X轴之间的夹角，逆时针为正。
假设车辆在任意时刻做直线运动或者绕某个点做圆周运动，并忽略悬架的作用，则可以得到车辆的转向运动模型，其中，(Xr，Yr)和(Xf，Yf)分别为车辆后轴中心和前轴中心在惯性坐标系下的坐标，vr为车辆在后轴中心处的速度，l为轴距，R为后轴中心的瞬时转向半径，δf为前轮偏角。
在后轴行驶轴心(Xr，Yr)处，速度为
前、后轴的运动学约束为
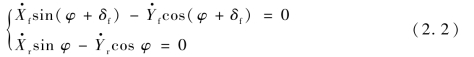
由式(2.1)和式(2.2)联合可得
根据前后轮的几何关系可得
(www.xing528.com)
将式(2.3)和式(2.4)代入式(2.2)，可解得横摆角速度为
其中，ω为车辆横摆角速度；同时，由ω和车速vr可得到转向半径R和前轮偏角δf：
由式(2.3)和式(2.5)可得到车辆运动学模型为
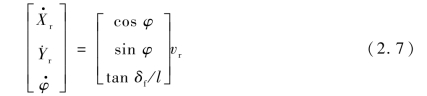
该模型可被进一步表示为更为一般的形式：
其中，状态量ξkin=[Xr，Yr，φ]T，控制量ukin=[vr，δf]T。在无人驾驶车辆的路径跟踪控制过程中，往往希望以[vr，ω]作为控制量，将式(2.5)代入式(2.7)中，则该车辆运动学模型可以被转换为如下形式：
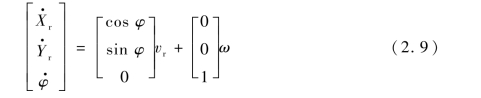
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
